Amplitude-Encoding Assignment
Amplitude-encoding assignment represents the evaluation of an expression over a quantum variable in the amplitudes of the resulting state. The target qubit serves as an indicator for the success of the computation. Supported expressions include a number of useful math functions, including trigonometric functions and multiplicative invert (\(x^{-1}\)).
Syntax
target-var *= expression
expression supports quantum numeric subscripts: [0, 1, 2, 3][n] or
lookup_table[n] where lookup_table is an array of classical real numbers
and n is an unsigned quantum integer.
target-var *= expression
expression supports quantum numeric subscripts:
subscript([0, 1, 2, 3], n) or lookup_table[n] where lookup_table is an
array of classical real numbers and n is an unsigned quantum integer.
Semantics
- target-var must be initialized prior to the assignment.
- Only a single quantum numeric variable is allowed in expression.
-
expression must evaluate to a real number in the domain [-1, 1]. Values that exceed this range are trimmed. Poles of the expression are ignored (set to 0). For example, given the expression
1/x, the zero state ofxis ignored, as it is undefined. -
For expression over quantum variable \(x\) that computes the function \(f(x)\), the operation performed by the statement is -
\(|x\rangle |0\rangle \rightarrow \sqrt{1-f^2(x)}|d\rangle |0\rangle + f(x)|x\rangle |1\rangle\)
Quantum Numeric Subscript Semantics
lookup_table[n]returns then'th item oflookup_table. Ifnis in superposition, so doeslookup_table[n].nmust be an unsigned quantum integer (is_signed=False, fraction_digits=0). The number of qubits innmust match the length oflookup_table:2 ** n.size == lookup_table.len.
Example
In the following example, the function \(f(x) = x^2\) is computed over a quantum variable x:
qfunc main(output x: qnum<5, False, 5>, output ind: qnum) {
allocate<5>(x);
hadamard_transform(x);
allocate<1>(ind);
ind *= x**2;
}
from classiq import QNum, qfunc, prepare_int, QBit
from classiq import (
Output,
QNum,
allocate,
qfunc,
hadamard_transform,
)
@qfunc
def main(x: Output[QNum[5, False, 5]], ind: Output[QNum]) -> None:
allocate(5, x)
hadamard_transform(x)
allocate(1, ind)
ind *= x**2
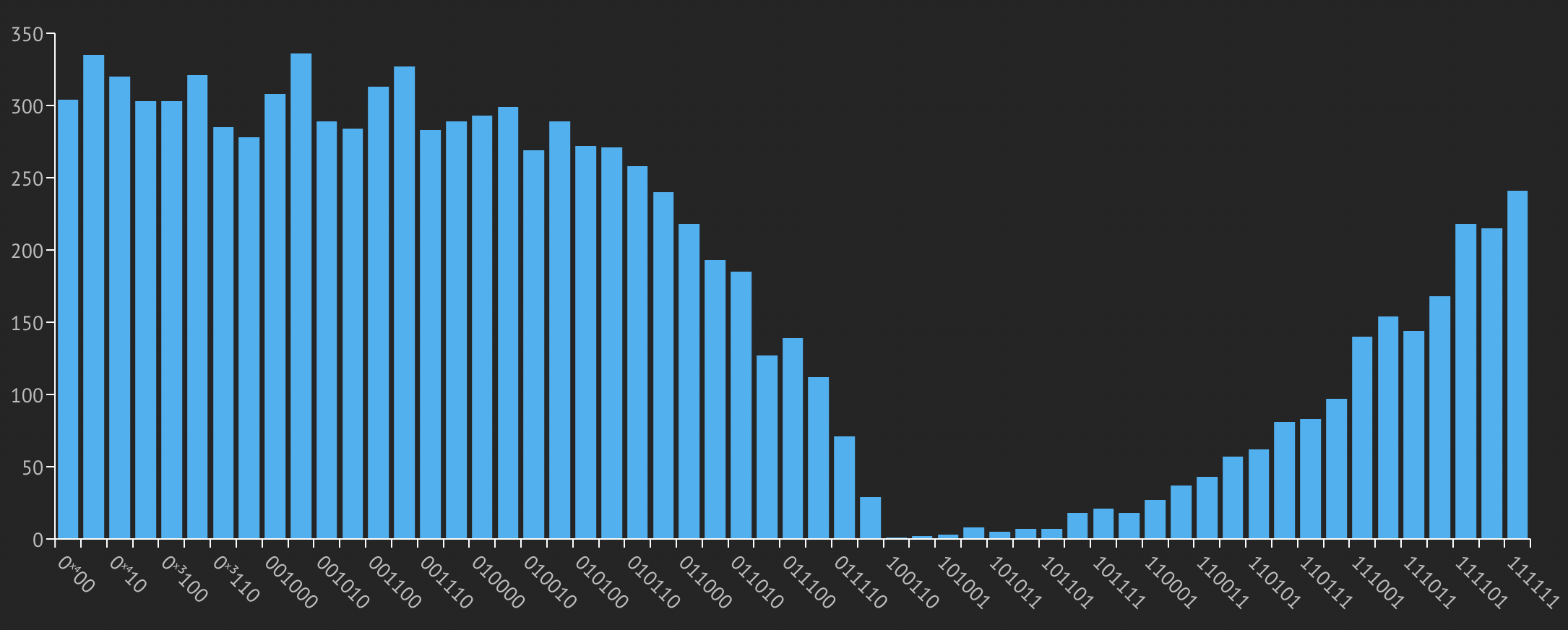
Synthesizing and executing this model results in the histogram shown below. States
with the variable ind sampled as 1 (on the right side of the histogram) have
probabilities corresponding to \((x^2)^2\). The probability of states with ind sampled
as 0 (on the left side of the histogram) correspond to \(\sqrt{1-(x^2)^2}\).