Design - Quantum Variables and Functions
In Qmod these types of quantum objects are represented by quantum variables: * Qubit (quantum bit)
* Written as `QBit` in the Python SDK
* Written as `qbit` in the native syntax
-
Qubit Array
A sequence of qubits, considered as a quantum register with a definite number of qubits.
- Written as
QArrayin the Python SDK - Written as
qbit[]in the native syntax
- Written as
-
Quantum Number
A qubit array (quantum register) that represents numbers. The numbers can be positive and negative integers, and can be fixed point (e.g., \(-5.25\)). The quantum number object has a definite number of qubits (as does every qubit array), and it has two properties for its numeric representation: if the number is signed or not (only positive or it represents negative numbers as well) and how many fractional digits it has (where is the decimal point).
- Written as
QNumin the Python SDK - Written as
qnumin the native syntax
- Written as
As explained in the Design page, you must declare and then initialize each quantum variable.
Concrete Example
First, understand these quantum variables through a concrete example.
The task is to design a quantum algorithm that flips the most significant bit (MSB) of a quantum number and then verify the new number.
What is the MSB?
In a binary representation, every number can be represented by a bit string (a sequence of zeros and ones). For example, the number $6$ can be represented by the bit string $110$. How? To understand it better, move one bit at a time and sum up the multiplication of the bit value times $2$ to the power of the bit position. Start with the rightmost bit, called the least significant bit (LSB) since its position is the 0th position. Sum $0\times 2^0 =0$ plus $1\times 2^1=2$ for the middle bit plus $1\times 2^2=4$ for the leftmost bit—the most significant bit (MSB) since its contribution to the sum is the most significant.This is how to handle it. Use the flip_msb function that receives a qubit array and flips its MSB. Call this function from the main function with some quantum number, and then verify the number using a qubit indicator.
The flip_msb function receives a QArray variable named reg (shortcut for register), and it flips its MSB using the X gate. This gate operates on the qubit at the last position of the qubit array reg where the counting starts from \(0\). The property len of the register reg is used as part of the function.
from classiq import QArray, X, qfunc
@qfunc
def flip_msb(reg: QArray):
X(reg[reg.len - 1])
qfunc flip_msb(reg: qbit[]) {
X(reg[reg.len - 1]);
}
Note that the variable reg is not initialized within the scope of the function flip_msb. This can be seen by the lack of the output declaration in the scope of the function, and it means that reg is initialized before it is called in the function.
Now to the main function.
There is only one variable as an argument for the function, which is the indicator, regardless of whether the MSB successfully flips. This is a qubit variable named indicator.
Within the function itself, declare and initialize a quantum number named x with \(4\) qubits. A general initialization with allocate initializes the quantum number to the state \(|0\rangle = |0000\rangle\). (This is true for both qubits and qubit arrays). The function flip_msb acts on the quantum number x, flipping its MSB and creating the state \(|1000\rangle = |8\rangle\).
NOTE
There is no need to declare if the quantum number is signed nor the number of its fractional digits. It is initialized with no fractional digits and is not signed (see [`allocate_num`](https://docs.classiq.io/latest/reference-manual/platform/qmod/language-reference/quantum-types/) for initializing a quantum number with these options).from classiq import Output, QBit, QNum, allocate
@qfunc
def main(indicator: Output[QBit]):
x = QNum("x")
allocate(4, x)
flip_msb(x)
indicator |= x == 8
qfunc main(output indicator: qbit) {
x: qnum;
allocate<4>(x);
flip_msb(x);
indicator = x == 8;
}
Finally, initialize the indicator qubit with the numeric assignment of the expression \(x==8\). That is, if you flip the MSB of x and transform it to the state |8\rangle, then the state of the qubit indicator equals \(|1\rangle\); otherwise, it equals $|0\rangle (i.e., indicating if the flip_msb operation succeeded).
Does `flip_msb` receive a quantum number or a quantum array?
Note that the function `flip_msb` is called with the quantum number `x` from the `main` function, whilst it is declared with a quantum array named `reg`. This demonstrates that quantum numbers can be cast to quantum arrays if they have the same number of qubits. In `main` you want to manipulate an arithmetic quantum object—a quantum number—whilst in the function `flip_msb` you just want to treat the quantum number as a qubit array, without its numeric description, and to apply a specific gate on one of its qubits.That's it! Now, to check if the MSB flipped successfully, synthesize and view the quantum program:
from classiq import create_model, show, synthesize
quantum_program = synthesize(create_model(main))
show(quantum_program)
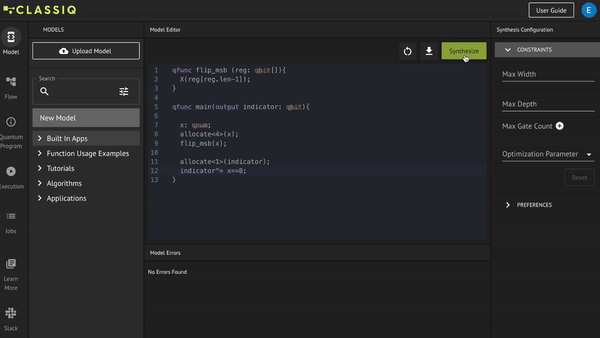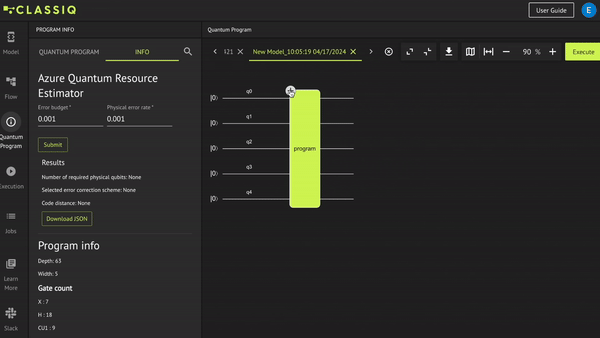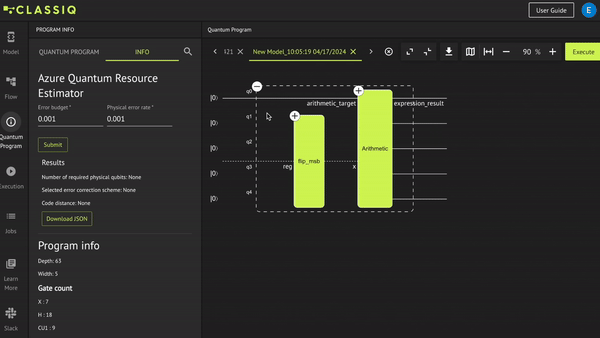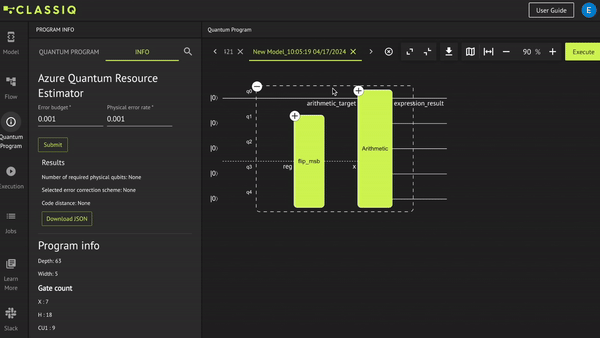
Execute the quantum program to receive the results:
from classiq import execute
job = execute(quantum_program)
results = job.result()[0].value.parsed_counts
print(results)
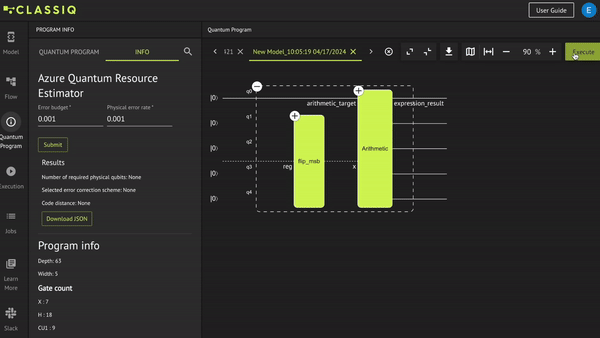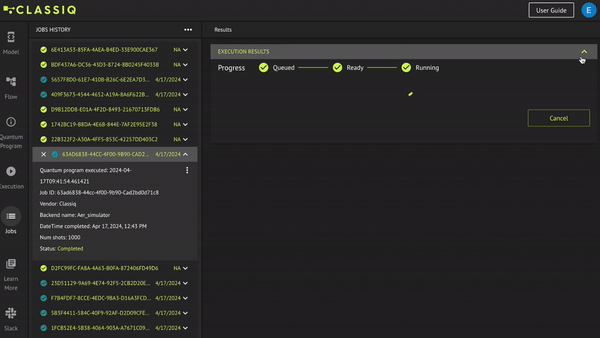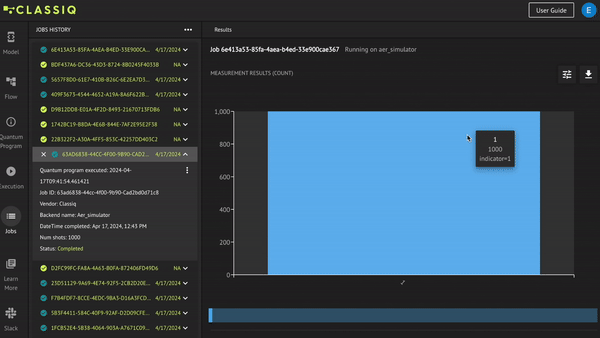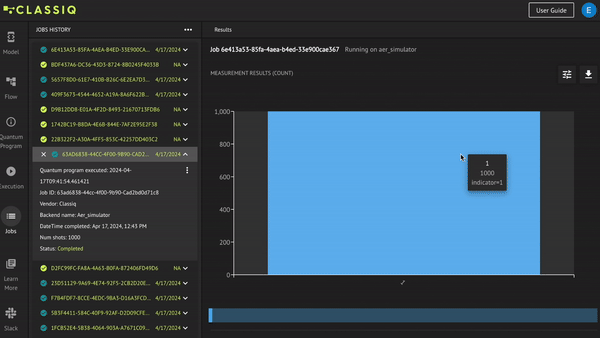
You did flip the MSB as indicated by the indicator variable.
Summary - Quantum Variables and Functions Guidelines
The following summarizes the main takeaways from the example in terms of quantum variables and functions:
- Types of quantum objects in Qmod: qubit, qubit array, and quantum number. Objects can be cast from one to another (as
xis cast from the quantum number in themainfunction to a qubit array with theflip_msbfunction). - Quantum objects are represented by quantum variables. Each variable needs to be declared and initialized before it is used. The initialization can be done in several ways, and here are two options: with the
allocatefunction (the initialization ofx) or with a numeric assignment (the initialization ofindicator). - Quantum variables that are arguments of a function can be declared with the
Outputmodifier and initialized within the scope of a function (likeindicatorin themainfunction). Without theOutputmodifier they must be initialized outside the scope of the function (likeregin theflip_msb) function. - Quantum variables can be declared and initialized within a function (like
xin themainfunction). - The quantum program is always generated from the
mainfunction, even when further quantum functions are used. The execution results of the quantum program are interpreted only for the arguments of themainfunction (likeindicatorin the above example).
Verify Your Understanding - Recommended Exercise
Create another quantum function flip_lsb that flips the least significant bit.
from classiq import write_qmod
write_qmod(create_model(main), "quantum_variables_and_functions")