Hidden-Shift Problem for Bent Functions
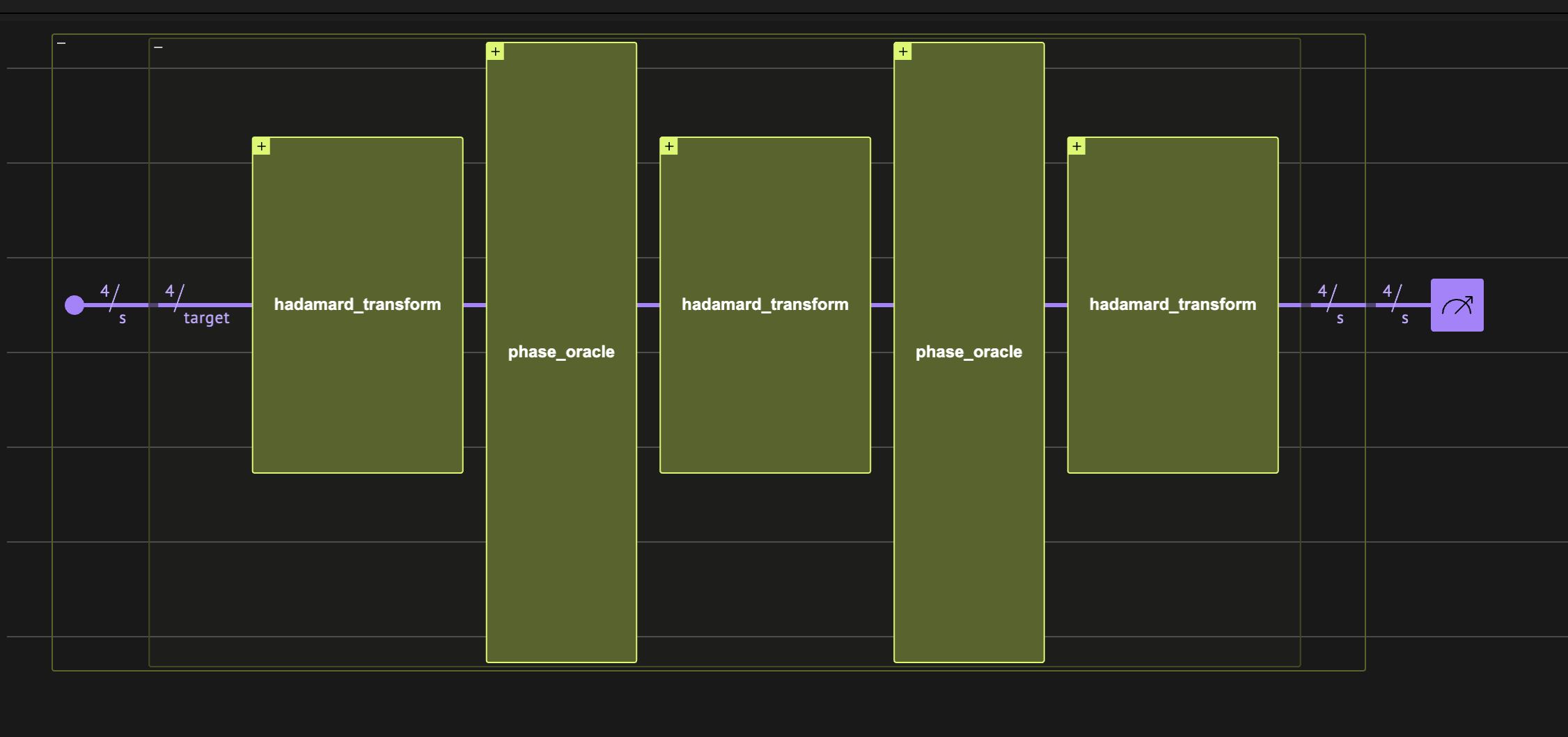
Here we implement the hidden shift algorithm for the family of Boolean bent functions using the Classiq platform.
Make sure we have all necessary packages:
!pip install galois
We assume we know how to implement the dual of \(f\) and get \(s\) according to the algorithm in [1]: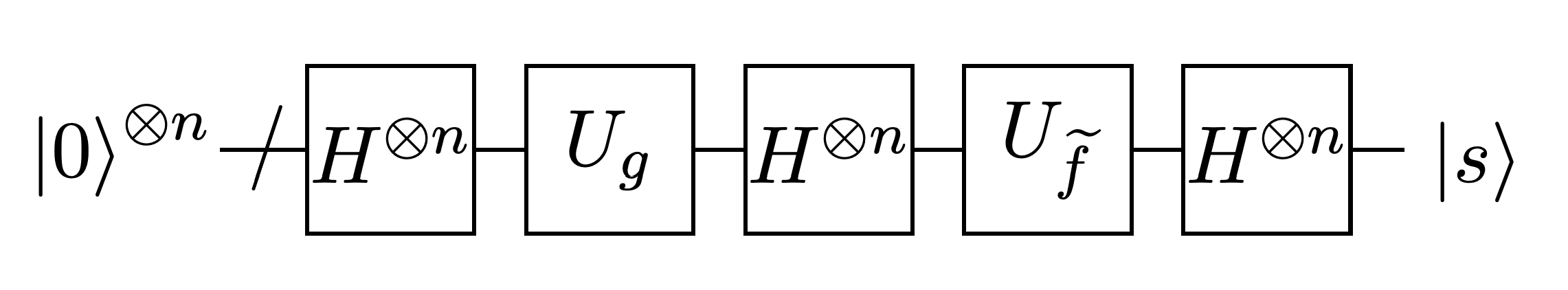
from classiq import *
@qfunc
def hidden_shift(
oracle: QCallable[QArray],
oracle_shifted: QCallable[QArray],
target: QArray,
) -> None:
hadamard_transform(target)
oracle_shifted(target)
hadamard_transform(target)
oracle(target)
hadamard_transform(target)
NUM_VARIABLES = 4
@qfunc
def main(s: Output[QArray]) -> None:
@qfunc
def arith_func(vars: QArray[QBit, NUM_VARIABLES], res: QBit):
res ^= (vars[0] & vars[1]) ^ (vars[2] & vars[3])
@qfunc
def arith_func_shifted(vars: QArray[QBit, NUM_VARIABLES], res: QBit):
res ^= ((vars[0] ^ 1) & vars[1]) ^ (vars[2] & vars[3])
allocate(NUM_VARIABLES, s)
hidden_shift(
lambda y: phase_oracle(arith_func, y),
lambda y: phase_oracle(arith_func_shifted, y),
s,
)
constraints = Constraints(optimization_parameter="width")
qmod_simple = create_model(main, constraints, out_file="hidden_shift_simple")
qprog_simple = synthesize(qmod_simple)
show(qprog_simple)
Quantum program link: https://platform.classiq.io/circuit/2yiRf4UKww8cZnqapBhyrgVYvNU
sample_results_simple = execute(qprog_simple).result_value()
sample_results_simple.counts_of_output("s")
{'1000': 2048}
More Complex Functions
We take a Maiorana-McFarland function with random permutation on the y and h function is the and operation between all the y-variables.
import random
from functools import reduce
import numpy as np
NUM_VARIABLES = 16
# Define the list
my_list = list(range(NUM_VARIABLES // 2))
# Get a random permutation
random.seed(1)
random.shuffle(my_list)
# Create a permutation dict and its inverse
perm_dict = {i: my_list[i] for i in range(NUM_VARIABLES // 2)}
inverse_perm_dict = {v: k for k, v in perm_dict.items()}
def h(y):
return reduce(lambda a, b: a & b, [y[i] for i in range(NUM_VARIABLES // 2)])
def h_dual(x):
return reduce(
lambda a, b: a & b, [x[inverse_perm_dict[i]] for i in range(NUM_VARIABLES // 2)]
)
def f_func(x, y):
return (
reduce(
lambda a, b: a ^ b,
[x[i] & y[perm_dict[i]] for i in range(NUM_VARIABLES // 2)],
)
) ^ h(y)
def f_dual_func(x, y):
return (
reduce(
lambda a, b: a ^ b,
[x[inverse_perm_dict[i]] & y[i] for i in range(NUM_VARIABLES // 2)],
)
) ^ h_dual(x)
def shifted(x, y, bits):
x = [x[i] for i in range(NUM_VARIABLES // 2)]
y = [y[i] for i in range(NUM_VARIABLES // 2)]
for bit in bits:
if bit < NUM_VARIABLES >> 2:
x[bit] = x[bit] ^ 1
else:
bit = bit - NUM_VARIABLES // 2
y[bit] = y[bit] ^ 1
return f_func(x, y)
shifted_bits = [1, 3, 9]
g_func = lambda x, y: shifted(x, y, shifted_bits)
Creating the Circuit
@qfunc
def g_qfunc(s: QArray, res: QBit):
res ^= g_func(s[0 : NUM_VARIABLES // 2], s[NUM_VARIABLES // 2 : s.len])
@qfunc
def f_dual_qfunc(s: QArray, res: QBit):
res ^= f_dual_func(s[0 : NUM_VARIABLES // 2], s[NUM_VARIABLES // 2 : s.len])
@qfunc
def f_qfunc(s: QArray, res: QBit):
res ^= f_func(s[0 : NUM_VARIABLES // 2], s[NUM_VARIABLES // 2 : s.len])
@qfunc
def main(s: Output[QArray]) -> None:
allocate(NUM_VARIABLES, s)
hidden_shift(
lambda y: phase_oracle(f_dual_qfunc, y),
lambda y: phase_oracle(g_qfunc, y),
s,
)
qmod_complex = create_model(
main, constraints=constraints, out_file="hidden_shift_complex"
) # same constraints
qprog_complex = synthesize(qmod_complex)
show(qprog_complex)
Quantum program link: https://platform.classiq.io/circuit/2yiVd3JYMKzpIKswXKVy0OEwhx1
sample_results_complex = execute(qprog_complex).result_value()
sample_results_complex.counts_of_output("s")
{'0101000001000000': 2048}
expected_s = "".join("1" if i in shifted_bits else "0" for i in range(NUM_VARIABLES))
assert list(sample_results_complex.counts_of_output("s").keys())[0] == expected_s
And indeed we got the correct shift!
Hidden Shift Without the Dual Function
We now use the second algorithm described in [2]. This algorithm only requires implementing \(f\) and not its dual; however, it requires \(O(n)\) samples from the circuit.
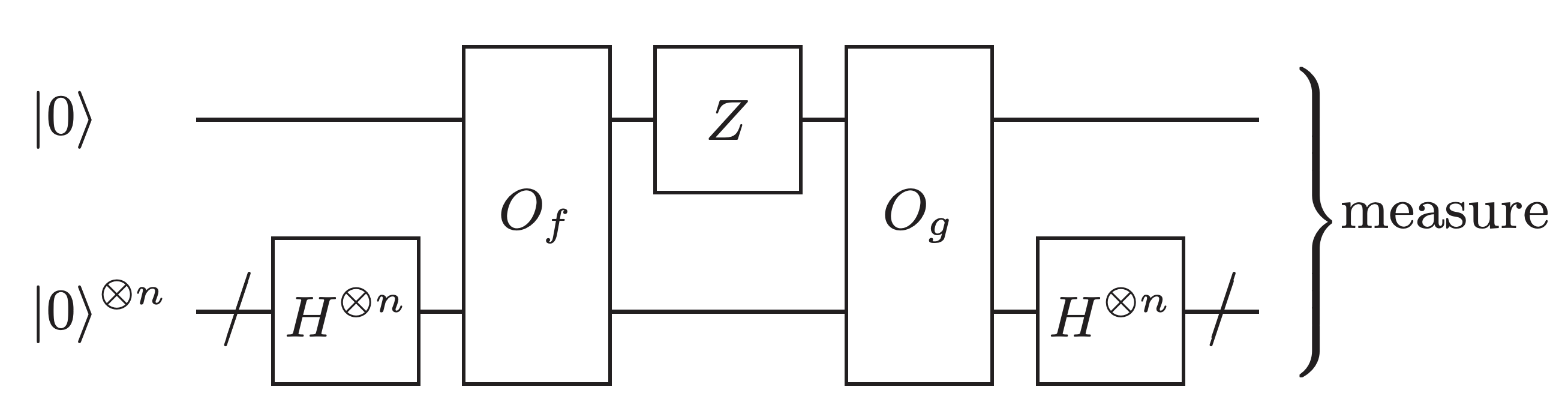
@qfunc
def hidden_shift_no_dual(
oracle: QCallable[QArray, QBit],
oracle_shifted: QCallable[QArray, QBit],
target: QArray,
ind: QBit,
) -> None:
hadamard_transform(target)
oracle(target, ind)
Z(ind)
oracle_shifted(target, ind)
hadamard_transform(target)
NUM_VARIABLES = 16
@qfunc
def main(target: Output[QArray], ind: Output[QBit]) -> None:
allocate(NUM_VARIABLES, target)
allocate(ind)
hidden_shift_no_dual(f_qfunc, g_qfunc, target, ind)
qmod_no_dual = create_model(
main, constraints=constraints, out_file="hidden_shift_no_dual"
) # same constraints
qprog_no_dual = synthesize(qmod_no_dual)
show(qprog_no_dual)
Quantum program link: https://platform.classiq.io/circuit/2yiVkcO51YjwXuebXL7vviao21H
sample_results_no_dual = execute(qprog_no_dual).result_value()
Out of the sampled results, we look for \(n\) independent samples, from which we can extract s. One thousand samples should be enough with a very high probability.
# The galois library is a package that extends NumPy arrays to operate over finite fields.
# we will use it as our equations are binary equations
import galois
# here we work over Boolean arithmetics - F(2)
GF = galois.GF(2)
def is_independent_set(vectors):
matrix = GF(vectors)
rank = np.linalg.matrix_rank(matrix)
if rank == len(vectors):
return True
else:
return False
samples = [
([int(i) for i in u], int(b))
for u, b in sample_results_no_dual.counts_of_multiple_outputs(
["target", "ind"]
).keys()
]
ind_v = []
ind_b = []
for v, b in samples:
if is_independent_set(ind_v + [v]):
ind_v.append(v)
ind_b.append(b)
if len(ind_v) == len(v):
# reached max set
break
assert len(ind_v) == len(v)
We now solve the equation and extract \(s\):
A = np.array(ind_v)
b = np.array(ind_b)
# Solve the linear system
s = np.linalg.solve(GF(A), GF(b))
s
GF([0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0], order=2)
And we successfully received the same shift.
assert "".join(str(i) for i in s) == expected_s
References
[1]: Quantum algorithms for highly non-linear Boolean functions