Skip to content

Introducing quantum functions with Quantum Monte Carlo Integration

View on GitHub Experiment in the IDE

In this tutorial we introduce how to write custom quantum functions with Classiq, and subsequently use them for more complex functions/algorithms. This will be illustrated on a specific use-case of Quantum Monte Carlo Integration (QMCI). The example below demonstrates how we can exploit various concepts of modeling quantum algorithms with Classiq when building our own functions.

QMCI

We start with a brief introduction to the quantum algorithm treated in this tutorial.

Monte Carlo integration refers to estimating expectation values of a function \(f(x)\), where \(x\) is a random variable drawn from some known distribution \(p\):

\begin{equation} \tag{1} E_{p}(x) = \int f(x)p(x) dx. \end{equation} Such evaluations appear in the context of option-pricing or credit risk-analysis.

The basic idea of QMCI assumes that we have a quantum function \(A\), which, for a given \(f\) and \(p\), loads the following state of \(n+1\) qubits: \begin{align} \tag{2} A|0\rangle_n|0\rangle = \sum^{2^n-1}{i=0} \sqrt{f_i} \sqrt{p_i}|i\rangle_n|1\rangle + \sum^{2^n-1}|\psi_0\rangle, \end{align} where it is understood that the first } \sqrt{1-f_i} \sqrt{p_i}|i\rangle_n|0\rangle = \sqrt{a}|\psi_1\rangle+\sqrt{1-a^2\(2^n\) states represent a discretized space of \(x\), and that \(0\leq f(x)\leq 1\). Then, by applying Amplitude Estimation (AE) algorithm for the "good-state" \(|\psi_1 \rangle\), we can estimate its amplitude

\[a = \sum^{2^n-1}_{i=0} f_i p_i.\]

The QMCI algorithm can be separated into two parts: 1) Constructing a Grover operator for the specific problem--- this will be done here almost from scratch. 2) Applying AE algorithm based on the Grover operator [1]--- this will be done by calling Classiq's Quantum Phase Estimation (QPE) function.

Specific use-case for the tutorial

For simplicity we will consider a simple use-case. We take a probability distribution on the integers $$ \tag{3} p_i = \frac{i}{\mathcal{N}} \text{ for } i\in {0,\dots 2^3-1},

\[where $\mathcal{N}$ is a normalization constant, and we would like to evaluate the expectation value of the function\]

\tag{4} f(x) = \sin^2(0.25x+0.2).

\[Therefore, the value we want to evaluate is:\]

a= \frac{1}{\mathcal{N}} \sum^7_{k=0} \sin^2(0.25k+0.2) k \approx 0.834. $$

1. Building the corresponding Grover Operator

Quantum Functions

The following example will demonstrate how to define QMOD functions by writing a Python function decorated with the @qfunc decorator. The typical workflow for defining a quantum function: 1. Specifying the function signature: The @qfunc decorator relies on Python's type-hint mechanism to extract the signature of the QMOD function from the argument list of the Python function. 2. Specifying the function body: A function decorated with @qfunc is executed by the Python interpreter to construct the body of the QMOD function. Inside it, you can do one of the following:

- Call other `@qfuncs` to insert the corresponding quantum function calls into the body of the resulting QMOD function

- Introduce local quantum variables, by instantiating a quantum type

- Use arithmetic and in-place assignment operators to insert special quantum statements into the function

We can start with relevant imports

import matplotlib.pyplot as plt

from classiq import (
    Constraints,
    H,
    Output,
    Pauli,
    QArray,
    QBit,
    QNum,
    U,
    X,
    Z,
    allocate,
    allocate_num,
    bind,
    control,
    create_model,
    execute,
    inplace_prepare_state,
    invert,
    linear_pauli_rotations,
    qfunc,
    qpe,
    set_constraints,
    show,
    synthesize,
    within_apply,
)

Grover operator for QMCI

The Grover operator suitable for QMCI is defined as follows:

\[Q\equiv - S_{\psi_1} A^{\dagger} S_0 A,\]

with \(S_0\) and \(S_{\psi_1}\) being reflection operators around the zero state \(|0\rangle_n|0\rangle\) and the good-state \(|\psi_1\rangle\), respectively, and the function \(A\) is defined in Eq. (2).

In subsections (1.1)-(1.3) below we build each of the quantum sub-functions, and then in subsection (1.4) we combine them to define a complete Grover operator. On the way we introduce several concepts of functional modeling which allow Classiq's Synthesis Engine to reach better optimized circuits.

1.1) The state loading \(A\) function

We start with constructing the \(A\) operator in Eq. (2). We define a quantum function and give it the name state_loading

The function's signature declares two arguments: 1. A quantum register io declared as QArray[QBit] (an array of qubits with an unspecified size): will be used to represent the discretization of space 2. A quantum register ind of size 1 declared as QBit to indicate the good state.

Next, we construct the logic flow of the state_loading function. The function body consists of 2 quantum function calls: load_probabilities followed by amplitude_loading

  • As can be seen from Eq. (2), the load_probabilities function is constructed using Classiq's inplace_prepare_state function call on \(n=3\) qubits with probabilities \(p_i\)

  • The amplitude_loading body consists of a function call to Classiq's linear_pauli_rotations. The linear_pauli_rotations is used to load the amplitude of the function $ f(x) = sin^2(0.25 x + 0.2) $.

    Note: the amplitude should be \(sin\) so the probability would be \(sin^2\).

    The function uses an auxiliary qubit that is utilized so that the desired probability will reflect on the auxiliary qubit if it is in the |1> state.

    We will use the function with the Pauli Y matrix and enter the appropriate slope and offset to achieve the right parameters.

We will define the probabilities according to our specific problem described by Eqs. (3-4)

import numpy as np

sp_num_qubits = 3
probabilities = np.linspace(0, 1, 2**sp_num_qubits) / sum(
    np.linspace(0, 1, 2**sp_num_qubits)
)


slope = 0.5
offset = 0.4


@qfunc
def load_probabilities(state: QArray[QBit]):
    inplace_prepare_state(probabilities.tolist(), 0, state)


@qfunc
def amplitude_loading(io: QArray[QBit], ind: QBit):
    linear_pauli_rotations(
        bases=[Pauli.Y.value], slopes=[slope], offsets=[offset], x=io, q=ind
    )


@qfunc
def state_loading(io: QArray[QBit], ind: QBit):
    load_probabilities(io)
    amplitude_loading(io=io, ind=ind)

To examine our function we define a quantum main function from which we can build a model, synthesize and view the quantum program created:

@qfunc
def main(res: Output[QArray[QBit]], ind: Output[QBit]):
    allocate(sp_num_qubits, res)
    allocate(1, ind)
    state_loading(res, ind)


model = create_model(main)
qprog = synthesize(model)
show(qprog)

Opening: https://platform.classiq.io/circuit/34ad642f-d5bb-4768-adce-74bbac142f64?version=0.41.0.dev39%2B79c8fd0855

1.2) \(S_{\psi_1}\) function - The good state oracle

The next quantum function we define is the one which reflects around the good state: any \(n+1\) state in which the ind register is at state \(|1\rangle\). This function can be simply constructed with a ZGate on the ind register. 

@qfunc
def good_state_oracle(ind: QBit):
    Z(ind)

1.3) \(S_{0}\) function - The Grover Diffuser

In order to implement the Grover Diffuser we aim to perform a controlled-Z operation on the \(|0>^n\) state.

We can define a zero_oracle quantum function with the io and ind registers as its arguments.

The within_apply operator takes two function arguments - compute and action, and invokes the sequence compute(), action(), and invert(compute()). Quantum objects that are allocated and prepared by compute are subsequently uncomputed and released.

The control condition is a logical expression over a quantum variable. Currently, expressions are restricted to the form <var> == <classical-expression>, where both <var> and <classical-expression> are integer types.

@qfunc
def prepare_minus(q: QBit):
    X(q)
    H(q)


@qfunc
def zero_oracle(x: QNum, ind: QBit):
    within_apply(lambda: prepare_minus(ind), lambda: control(x == 0, lambda: X(ind)))

One can verify that: \begin{eqnarray} |00\dots0\rangle \xrightarrow[{\rm ctrl(-Z)(target=q_0, ctrl=q_1\dots q_n)}]{} -|00\dots0\rangle, \ |10\dots0\rangle \xrightarrow[{\rm ctrl(-Z)(target=q_0, ctrl=q_1\dots q_n)}]{} |10\dots0\rangle, \ |11\dots0\rangle \xrightarrow[{\rm ctrl(-Z)(target=q_0, ctrl=q_1\dots q_n)}]{} |11\dots0\rangle,\ |11\dots1\rangle \xrightarrow[{\rm ctrl(-Z)(target=q_0, ctrl=q_1\dots q_n)}]{} |11\dots1\rangle, \end{eqnarray} which is exactly the functionality we want.

1.4) \(Q\) function - The Grover operator

We can now define a complete Grover operator \(Q\equiv -S_{\psi_1} A^{\dagger} S_0 A\). We will do this in a single code block that will call the following: 1. The good state oracle (good_state_oracle) 2. THe inverse of the state preparation (state_loading) 3. The Diffuser (zero_oracle) 4. The state preparation (state_loading)

Note:

  • Stages 2-4 are implemented by utilizing the within_apply operator

  • We add a global phase of -1 to the full operator by using the atomic gate level function U

@qfunc
def my_grover_operator(state: QArray[QBit]):
    io = QArray[QBit]("io", length=state.len - 1)
    ind = QBit("ind")
    bind(state, [ind, io])
    good_state_oracle(ind=ind)
    within_apply(
        lambda: invert(lambda: state_loading(io=io, ind=ind)),
        lambda: zero_oracle(io, ind),
    )
    U(0, 0, 0, np.pi, ind)
    bind([ind, io], state)
Let us look at the my_grover_operator function we created
@qfunc
def main(state: Output[QArray[QBit]]):
    io = QArray[QBit]("io")
    ind = QBit("ind")
    allocate(sp_num_qubits, io)
    allocate(1, ind)
    bind([ind, io], state)
    my_grover_operator(state)


model = create_model(main)
qprog = synthesize(model)
show(qprog)

Opening: https://platform.classiq.io/circuit/e0a2e845-a21b-4c68-9d37-ae49d43ede11?version=0.41.0.dev39%2B79c8fd0855

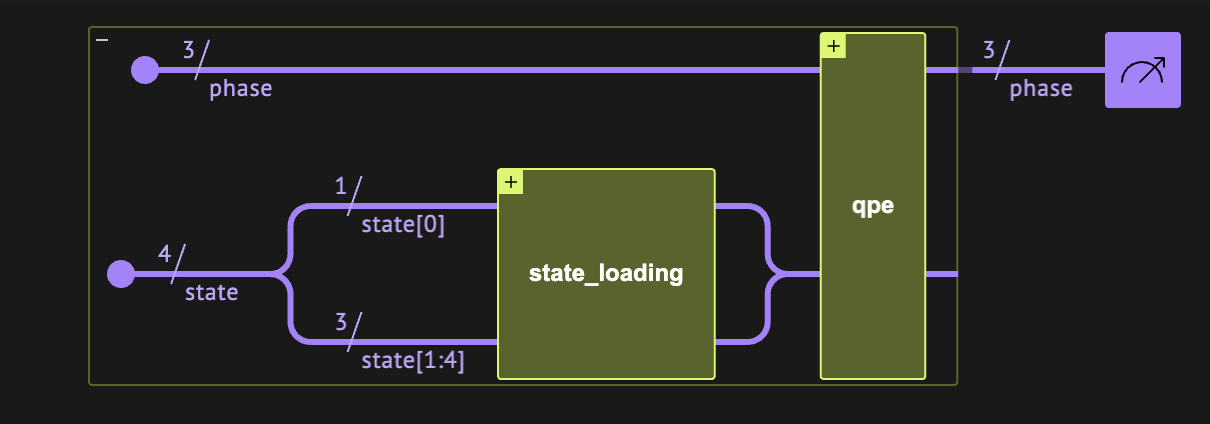
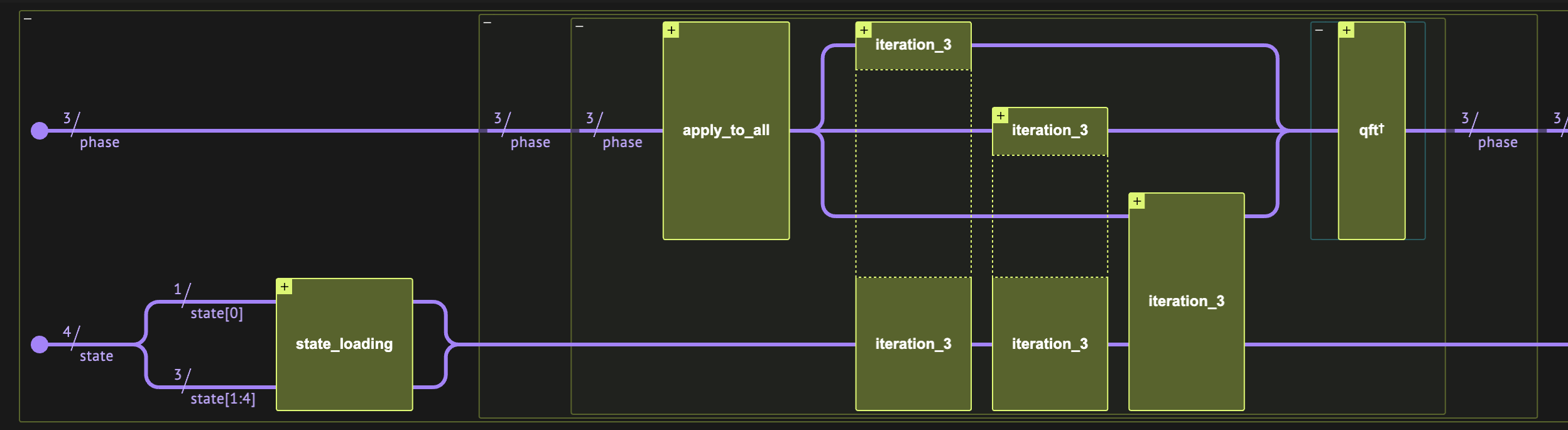
2. Applying Amplitude Estimation (AE) with Quantum Phase Estimation (QPE)

Below we apply a basic AE algorithm which is based on QPE. The idea behind this Algorithm is the following:

The state \(A|0\rangle_n|0\rangle\) is spanned by two eigenvectors of our Grover operator \(Q\), with the two corresponding eigenvalues \begin{equation} \tag{5} \lambda_{\pm}=\exp\left(\pm i2\pi \theta \right), \qquad \sin^2 \left(\pi \theta\right)\equiv a. \end{equation} Therefore, if we apply a QPE on \(A|0\rangle_n|0\rangle\) we will have these two eigenvalues encoded in the QPE register, however, both give the value of \(a\), so there is no ambiguity here.

To find \(a\) we are going to build a simple quantum model: we apply \(A\) on a quantum register of size \(n+1\) initialized to zero, and then apply Classiq's QPE with the my_grover_operator we defined.

Below is the main function from which we can build our model and synthesize it. In particular, we define the output register phase as QNum to hold the phase register output of the QPE. We choose a QPE with phase register of size 3, governing the accuracy of our Phase-, and thus Amplitude-, Estimation. 

n_qpe = 3


@qfunc
def main(phase: Output[QNum]):
    io = QArray[QBit]("io")
    ind = QBit("ind")
    allocate(sp_num_qubits, io)
    allocate(1, ind)
    state_loading(io=io, ind=ind)
    state = QArray[QBit]("state")
    bind([ind, io], state)
    allocate_num(n_qpe, False, n_qpe, phase)
    qpe(unitary=lambda: my_grover_operator(state=state), phase=phase)
    bind(state, [ind, io])


model = create_model(main)
model = set_constraints(model, Constraints(max_width=9))
qprog = synthesize(model)
show(qprog)

Opening: https://platform.classiq.io/circuit/6ac9f51e-f111-4e96-ba45-975b333c0418?version=0.41.0.dev39%2B79c8fd0855

We can simply export our model to a .qmod file:

from classiq import write_qmod

write_qmod(model, "qmc_user_defined", decimal_precision=10)

Finally, we execute the circuit and measure the approximated amplitude

We start with a simple execution on a simulator

res = execute(qprog).result()[0].value

We identify \(|\lambda_0,\lambda_1\dots \lambda_{m-1}\rangle_m=\frac{1}{2^m}\sum^{m-1}_{i=0}\lambda_i 2^i\), whose mapping can be done as follows:

## mapping between register string to phases
phases_counts = dict(
    (sampled_state.state["phase"], sampled_state.shots)
    for sampled_state in res.parsed_counts
)

Plotting the resulting histogram we see two phase values with high probability (however, both corresponds to the same amplitude \(a\))

plt.bar(phases_counts.keys(), phases_counts.values(), width=0.1)
plt.xticks(rotation=90)
print("phase with max probability: ", max(phases_counts, key=phases_counts.get))

phase with max probability:  0.625

png

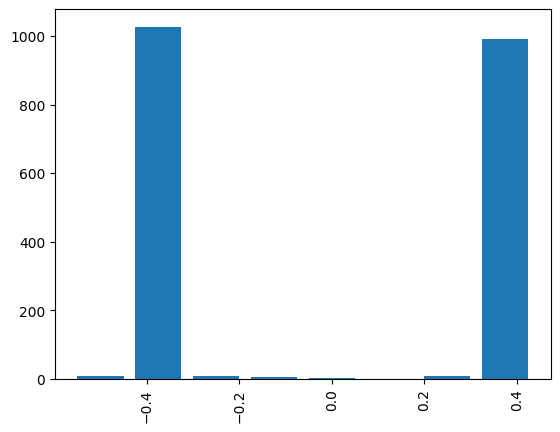
Recall the relation in Eq. (5), we can read the amplitude \(a\) from the phase with max probability, and compare to the expected amplitude:

print(
    "measured amplitude: ",
    np.sin(np.pi * max(phases_counts, key=phases_counts.get)) ** 2,
)
print(
    "exact amplitude: ",
    sum(np.sin(0.5 * n / 2 + 0.4 / 2) ** 2 * probabilities[n] for n in range(2**3)),
)

measured amplitude:  0.8535533905932737
exact amplitude:  0.8338393824876795

References

[1]: Brassard, G., Hoyer, P., Mosca, M., & Tapp, A. (2002). Quantum Amplitude Amplification and Estimation. Contemporary Mathematics, 305, 53-74.