Skip to content

Amplitude-Encoding Assignment

Amplitude-encoding assignment represents the evaluation of an expression over a quantum variable in the amplitudes of the resulting state. The target qubit serves as an indicator for the success of the computation. Supported expressions include a number of useful math functions, including trigonometric functions and multiplicative invert (\(x^{-1}\)).

Syntax

target-var *= expression

expression supports quantum numeric subscripts: [0, 1, 2, 3][n] or lookup_table[n] where lookup_table is an array of classical real numbers and n is an unsigned quantum integer.

target-var *= expression
OR
assign_amplitude(expression, target-var)

Notes

  • The operator syntax and the function call syntax are equivalent. The operator syntax is typically easier to read, but it cannot be used directly in lambda expressions, where the function call syntax should be used.

Semantics

  • target-var must be initialized prior to the assignment.
  • expression consists of a single quantum scalar variable, numeric constant literals, and classical scalar variables, composed using arithmetic operators and math functions. See the set of supported operators under Numeric Assignment. In addition to these operators, the functions in package qmod.symbolic are also supported.
  • expression must evaluate to a real number in the domain [-1, 1]. Values that exceed this range are trimmed. Poles of the expression are ignored (set to 0). For example, given the expression 1/x, the zero state of x is ignored, as it is undefined.
  • For expression over quantum variable \(x\) that computes the function \(f(x)\), the operation performed by the statement is -

\(|x\rangle |0\rangle \rightarrow \sqrt{1-f^2(x)}|x\rangle |0\rangle + f(x)|x\rangle |1\rangle\)

Examples

Example 1

In the following example, the function \(f(x) = x^2\) is computed over a quantum variable x:

qfunc main(output x: qnum<5, UNSIGNED, 5>, output ind: qbit) {
  allocate(x);
  hadamard_transform(x);
  allocate(ind);
  ind *= x**2;
}

from classiq import *


@qfunc
def main(x: Output[QNum[5, UNSIGNED, 5]], ind: Output[QBit]) -> None:
    allocate(x)
    hadamard_transform(x)
    allocate(ind)
    ind *= x**2

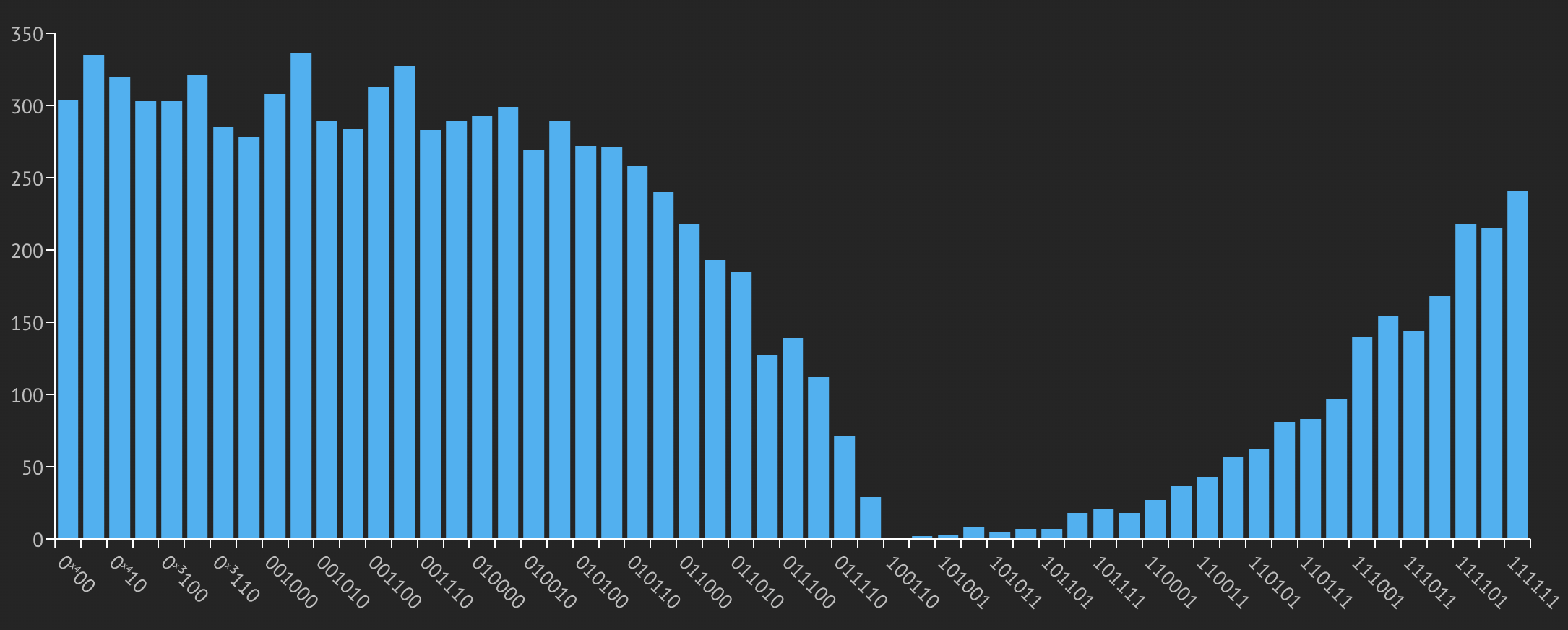
Synthesizing and executing this model results in the histogram shown below. States with the variable ind sampled as 1 (on the right side of the histogram) have probabilities corresponding to \((x^2)^2\). The probability of states with ind sampled as 0 (on the left side of the histogram) correspond to \(1-(x^2)^2\).

amplitude_encoding_result.png

Example 2: Quantum Subscript

In this example, we demonstrate amplitude-encoding assignment with a quantum subscript expression, i.e., a classical list indexed by a quantum numeric variable.

qfunc main(output x: qnum<2>, output ind: qbit) {
  allocate(x);
  hadamard_transform(x);
  allocate(ind);
  ind *= [0.1, 0.2, 0.3, 0.4][x];
}

from classiq import *
from classiq.qmod.symbolic import subscript


@qfunc
def main(x: Output[QNum[2]], ind: Output[QBit]) -> None:
    allocate(x)
    hadamard_transform(x)
    allocate(ind)
    ind *= subscript([0.1, 0.2, 0.3, 0.4], x)