Number Partition Problem
Introduction
In the Number Partitioning Problem [1] we need to find how to partition a set of integers into two subsets of equal sums. In case such a partition does not exist, we can ask for a partition where the difference between the sums is minimal.
Mathematical formulation
Given a set of numbers \(S=\{s_1,s_2,...,s_n\}\), a partition is defined as \(P_1,P_2 \subset \{1,...,n\}\), with \(P_1\cup P_2=\{1,...,n\}\) and \(P_1\cap P_2=\emptyset\). In the Number Partitioning Problem we need to determine a partition such that \(|\sum_{j\in P_1}s_j-\sum_{j\in P_2}s_j|\) is minimal. A partition can be represented by a binary vector \(x\) of size \(n\), where we assign 0 or 1 for being in \(P_1\) or \(P_2\), respectively. The quantity we ask to minimize is \(|\vec{x}\cdot \vec{s}-(1-\vec{x})\cdot\vec{s}|=|(2\vec{x}-1)\cdot\vec{s}|\). In practice we will minimize the square of this expression.
Solving with the Classiq platform
We go through the steps of solving the problem with the Classiq platform, using QAOA algorithm [2]. The solution is based on defining a pyomo model for the optimization problem we would like to solve.
import networkx as nx
import numpy as np
import pyomo.core as pyo
from matplotlib import pyplot as plt
Building the Pyomo model from a graph input
We proceed by defining the Pyomo model that will be used on the Classiq platform, using the mathematical formulation defined above:
# we define a matrix which gets a set of integers s and returns a pyomo model for the partitioning problem
def partite(s) -> pyo.ConcreteModel:
model = pyo.ConcreteModel()
SetSize = len(s) # the set size
model.x = pyo.Var(
range(SetSize), domain=pyo.Binary
) # our variable is a binary vector
# we define a cost function
model.cost = pyo.Objective(
expr=sum(((2 * model.x[i] - 1) * s[i]) for i in range(SetSize)) ** 2,
sense=pyo.minimize,
)
return model
Myset = np.random.randint(1, 12, 10)
mylist = [int(x) for x in Myset]
print("This is my list: ", mylist)
set_partition_model = partite(mylist)
This is my list: [8, 8, 8, 5, 5, 6, 5, 6, 8, 11]
set_partition_model.pprint()
1 Set Declarations
x_index : Size=1, Index=None, Ordered=Insertion
Key : Dimen : Domain : Size : Members
None : 1 : Any : 10 : {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
1 Var Declarations
x : Size=10, Index=x_index
Key : Lower : Value : Upper : Fixed : Stale : Domain
0 : 0 : None : 1 : False : True : Binary
1 : 0 : None : 1 : False : True : Binary
2 : 0 : None : 1 : False : True : Binary
3 : 0 : None : 1 : False : True : Binary
4 : 0 : None : 1 : False : True : Binary
5 : 0 : None : 1 : False : True : Binary
6 : 0 : None : 1 : False : True : Binary
7 : 0 : None : 1 : False : True : Binary
8 : 0 : None : 1 : False : True : Binary
9 : 0 : None : 1 : False : True : Binary
1 Objective Declarations
cost : Size=1, Index=None, Active=True
Key : Active : Sense : Expression
None : True : minimize : ((2*x[0] - 1)*8 + (2*x[1] - 1)*8 + (2*x[2] - 1)*8 + (2*x[3] - 1)*5 + (2*x[4] - 1)*5 + (2*x[5] - 1)*6 + (2*x[6] - 1)*5 + (2*x[7] - 1)*6 + (2*x[8] - 1)*8 + (2*x[9] - 1)*11)**2
3 Declarations: x_index x cost
Setting Up the Classiq Problem Instance
In order to solve the Pyomo model defined above, we use the CombinatorialProblem python class. Under the hood it tranlates the Pyomo model to a quantum model of the QAOA algorithm, with cost hamiltonian translated from the Pyomo model. We can choose the number of layers for the QAOA ansatz using the argument num_layers, and the penalty_factor, which will be the coefficient of the constraints term in the cost hamiltonian.
from classiq import *
from classiq.applications.combinatorial_optimization import CombinatorialProblem
combi = CombinatorialProblem(
pyo_model=set_partition_model, num_layers=3, penalty_factor=10
)
qmod = combi.get_model()
write_qmod(qmod, "set_partition")
Synthesizing the QAOA Circuit and Solving the Problem
We can now synthesize and view the QAOA circuit (ansatz) used to solve the optimization problem:
qprog = combi.get_qprog()
show(qprog)
Opening: https://nightly.platform.classiq.io/circuit/aec5c205-9edc-4e25-9812-ce23575c5542?version=0.62.0.dev9
We also set the quantum backend we want to execute on:
from classiq.execution import *
execution_preferences = ExecutionPreferences(
backend_preferences=ClassiqBackendPreferences(backend_name="simulator"),
)
We now solve the problem by calling the optimize method of the CombinatorialProblem object. For the classical optimization part of the QAOA algorithm we define the maximum number of classical iterations (maxiter) and the \(\alpha\)-parameter (quantile) for running CVaR-QAOA, an improved variation of the QAOA algorithm [3]:
optimized_params = combi.optimize(execution_preferences, maxiter=80, quantile=0.7)
Optimization Progress: 70%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 56/80 [02:08<00:55, 2.29s/it]
We can check the convergence of the run:
plt.plot(combi.cost_trace)
plt.xlabel("Iterations")
plt.ylabel("Cost")
plt.title("Cost convergence")
Text(0.5, 1.0, 'Cost convergence')

Optimization Results
We can also examine the statistics of the algorithm. In order to get samples with the optimized parameters, we call the sample method:
optimization_result = combi.sample(optimized_params)
optimization_result.sort_values(by="cost").head(5)
| solution | probability | cost | |
|---|---|---|---|
| 139 | {'x': [0, 0, 1, 1, 1, 1, 1, 1, 0, 0]} | 0.001953 | 1.183052e-271 |
| 278 | {'x': [1, 1, 0, 0, 0, 0, 1, 1, 1, 0]} | 0.000977 | 1.183052e-271 |
| 545 | {'x': [1, 0, 1, 0, 0, 0, 0, 0, 1, 1]} | 0.000488 | 1.183052e-271 |
| 515 | {'x': [0, 0, 1, 0, 1, 0, 1, 1, 0, 1]} | 0.000488 | 1.183052e-271 |
| 438 | {'x': [0, 0, 0, 1, 1, 1, 0, 0, 1, 1]} | 0.000488 | 1.183052e-271 |
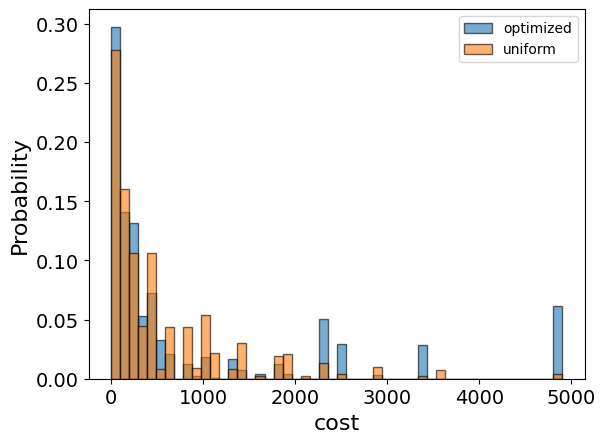
We will also want to compare the optimized results to uniformly sampled results:
uniform_result = combi.sample_uniform()
And compare the histograms:
optimization_result["cost"].plot(
kind="hist",
bins=50,
edgecolor="black",
weights=optimization_result["probability"],
alpha=0.6,
label="optimized",
)
uniform_result["cost"].plot(
kind="hist",
bins=50,
edgecolor="black",
weights=uniform_result["probability"],
alpha=0.6,
label="uniform",
)
plt.legend()
plt.ylabel("Probability", fontsize=16)
plt.xlabel("cost", fontsize=16)
plt.tick_params(axis="both", labelsize=14)
Let us plot the best solution:
best_solution = optimization_result.solution[optimization_result.cost.idxmin()]
p1 = [mylist[i] for i in range(len(mylist)) if best_solution["x"][i] == 0]
p2 = [mylist[i] for i in range(len(mylist)) if best_solution["x"][i] == 1]
print("P1=", p1, ", total sum: ", sum(p1))
print("P2=", p2, ", total sum: ", sum(p2))
print("difference= ", abs(sum(p1) - sum(p2)))
P1= [5, 6, 5, 8, 11] , total sum: 35
P2= [8, 8, 8, 5, 6] , total sum: 35
difference= 0
Lastly, we can compare to the classical solution of the problem:
from pyomo.opt import SolverFactory
solver = SolverFactory("couenne")
solver.solve(set_partition_model)
set_partition_model.display()
Model unknown
Variables:
x : Size=10, Index=x_index
Key : Lower : Value : Upper : Fixed : Stale : Domain
0 : 0 : 0.0 : 1 : False : False : Binary
1 : 0 : 0.0 : 1 : False : False : Binary
2 : 0 : 0.0 : 1 : False : False : Binary
3 : 0 : 1.0 : 1 : False : False : Binary
4 : 0 : 1.0 : 1 : False : False : Binary
5 : 0 : 1.0 : 1 : False : False : Binary
6 : 0 : 1.0 : 1 : False : False : Binary
7 : 0 : 1.0 : 1 : False : False : Binary
8 : 0 : 1.0 : 1 : False : False : Binary
9 : 0 : 0.0 : 1 : False : False : Binary
Objectives:
cost : Size=1, Index=None, Active=True
Key : Active : Value
None : True : 0.0
Constraints:
None
classical_solution = [pyo.value(set_partition_model.x[i]) for i in range(len(mylist))]
p1 = [mylist[i] for i in range(len(mylist)) if round(classical_solution[i]) == 0]
p2 = [mylist[i] for i in range(len(mylist)) if round(classical_solution[i]) == 1]
print("P1=", p1, ", total sum: ", sum(p1))
print("P2=", p2, ", total sum: ", sum(p2))
print("difference= ", abs(sum(p1) - sum(p2)))
P1= [8, 8, 8, 11] , total sum: 35
P2= [5, 5, 6, 5, 6, 8] , total sum: 35
difference= 0
References
[1]: Number Partitioning Problem (Wikipedia)
[2]: Farhi, Edward, Jeffrey Goldstone, and Sam Gutmann. "A quantum approximate optimization algorithm." arXiv preprint arXiv:1411.4028 (2014).
[3]: Barkoutsos, Panagiotis Kl, et al. "Improving variational quantum optimization using CVaR." Quantum 4 (2020): 256.