Skip to content

Control

The control statement applies a unitary operation conditionally, depending on a quantum state, and optionally a different one if the condition doesn't hold. The unitary operations are specified as nested statement blocks. The objects used in the statement blocks become entangled with the object used in the condition, so that any superposition in the state of the condition carries over to the operations in the statement blocks. The control statement could be viewed as the quantum equivalent of the classical if statement, with a then block and an optional else block.

The condition can be specified in one of two forms: as a single quantum variable, and as a quantum logical expression.

Syntax

control ( ctrl-var ) { statements } [else { else-statements }]

control ( ctrl-expression ) { statements } [else { else-statements }]

def control(
    ctrl: Union[SymbolicExpr, QBit, QArray[QBit]],
    stmt_block: Union[QCallable, Callable[[], None]],
    else_block: Union[QCallable, Callable[[], None], None] = None,
) -> None:
    pass

Semantics

  • ctrl-var (in the first variant) is a quantum variable of type qbit or qbit[], and ctrl-expression (in the second variant) is a logical expression over a quantum variable.
  • The statement block is applied if all the qubits in ctrl are in state \(|1\rangle\) (in the first variant), or if the ctrl-expression evaluates to true (in the second variant).
  • else-statements block is optional, and is applied if the negation of the condition holds, that is, if at least one of the qubits in ctrl is in state \(|1\rangle\) (in the first variant), or if the ctrl-expression evaluates to False (in the second variant).
  • Currently, there exists a single limitation on the expression: if ctrl-expression is an equality between a single variable and a classical expression, it is restricted to integers, meaning: In a ctrl-expression of the form <var> == <classical-expression>, <var> should be a qnum with zero fraction places or a qbit, and <classical-expression> should evaluate to an integer.
  • The same variable cannot occur both in the condition and inside the statement block. This restriction applies also to mutually exclusive slices of the same variable.
  • Quantum variables declared outside the control statement and used in its condition or inside its nested block must be initialized prior to it and remain initialized subsequently.

Examples

Example 1: Single-qubit control

In the following example, control statement applies function X on the variable target conditioned on a single qubit variable qb. Note that this is equivalent to using the built-in gate-level function CX.

qfunc main(output target: qbit) {
  qb: qbit;
  allocate(1, qb);
  H(qb);
  allocate(1, target);
  control (qb) {
    X(target);
  }
}

from classiq import H, Output, QBit, X, allocate, control, qfunc


@qfunc
def main(target: Output[QBit]) -> None:
    qb = QBit("qb")
    allocate(1, qb)
    H(qb)
    allocate(1, target)
    control(qb, lambda: X(target))

Synthesizing this model creates the quantum program shown below.

control_single_qubit.png

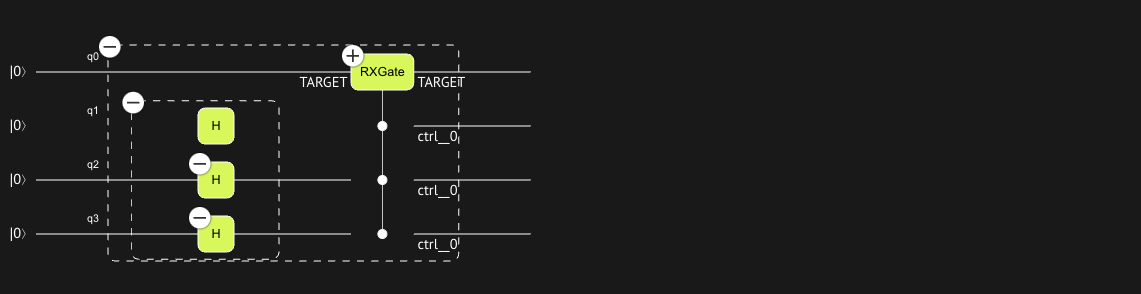
Example 2: Multi-qubit control

The next example shows how control can be similarly used with multi-qubit control variable. In this case target is rotated when the state of qba is the bit string 111.

qfunc main(output target: qbit) {
  qba: qbit[];
  allocate(3, qba);
  hadamard_transform(qba);
  allocate(1, target);
  control (qba) {
    RX(pi / 2, target);
  }
}

from sympy import pi
from classiq import *


@qfunc
def main(target: Output[QBit]) -> None:
    qba = QArray("qba")
    allocate(3, qba)
    hadamard_transform(qba)
    allocate(1, target)
    control(qba, lambda: RX(pi / 2, target))

Synthesizing this model creates the quantum program shown below.

control_multi_qubit.png

Example 3: Numeric equality condition

The following example demonstrates the use of control to rotate the state of a qubit by an angle determined by another quantum variable. In this case the condition compares the quantum variable with the repeat index.

qfunc switch_rx(x: qnum, target: qbit) {
  repeat (i: 4) {
    control (x == i) {
      RX(pi / (2 ** i), target);
    }
  }
}

qfunc main(output res: qbit) {
  allocate(1, res);
  x: qnum;
  x = 2;
  switch_rx(x, res);
}

from classiq import *
from classiq.qmod.symbolic import pi


@qfunc
def switch_rx(x: QNum, target: QBit) -> None:
    repeat(4, lambda i: control(x == i, lambda: RX(pi / 2**i, target)))


@qfunc
def main(res: Output[QBit]):
    allocate(1, res)
    x = QNum("x")
    x |= 2
    switch_rx(x, res)

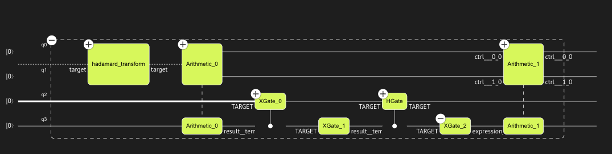
Synthesizing this model creates the following quantum program. Note how control is implemented as positive and negative controls in the respective numeric qubits.

control_value.jpg

Example 4: Arithmetic condition

The following example demonstrates the use of control to rotate the state of a qubit according to a condition imposed by another two quantum variables, x and y. Here, the condition filters quantum states such that y <= x[0] + x[1] + x[2].

qfunc switch_rx(x: qbit[], y: qnum, target: qbit) {
    control (y <= x[0] + x[1] + x[2]) {
      RX(pi / 3, target);
    }
}

qfunc main(output res: qbit) {
    allocate(1, res);
    x: qbit[3];
    y: qnum<3, UNSIGNED, 0>;
    allocate(3, x);
    allocate(3, y);
    hadamard_transform(x);
    hadamard_transform(y);
    switch_rx(x, y, res);
}

from classiq import *
from classiq.qmod.symbolic import pi


@qfunc
def switch_rx(x: QArray[QBit], y: QNum, target: QBit) -> None:
    control(x[0] + x[1] + x[2] >= y, lambda: RX(pi / 3, target))


@qfunc
def main(res: Output[QBit]) -> None:
    allocate(1, res)
    x: QArray = QArray("x", QBit, 3)
    y: QNum = QNum("y", 3, UNSIGNED, 0)
    allocate(3, x)
    allocate(3, y)
    hadamard_transform(x)
    hadamard_transform(y)
    switch_rx(x, y, res)

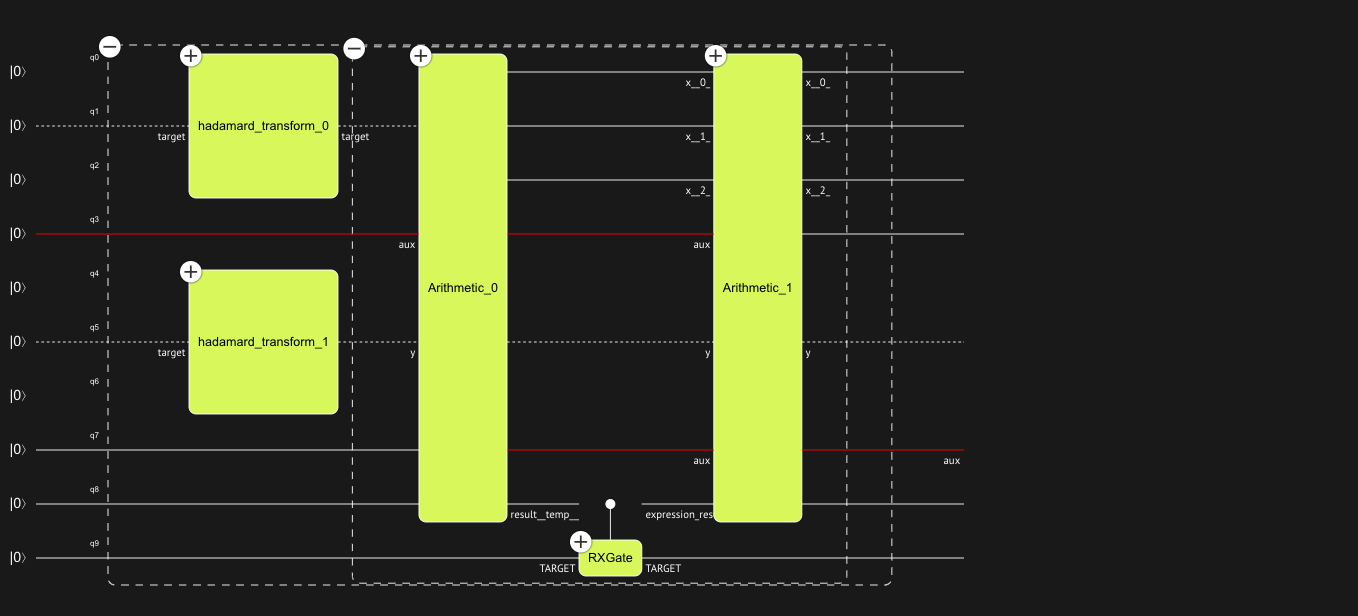
Synthesizing this model creates the following quantum program. Note how control is implemented as a result of an arithmetic computation. After applying the control operation, the arithmetic operation is un-computed.

control_arithmetic.jpg

Example 5: Control else

The following example demonstrates the use of the else block in the control statement. In this case, the else block applies an 'H' gate on the target qubit when the control condition is not met, instead of the 'X' gate, so when each qubit of the control variable is in state \(|1\rangle\), the bit is flipped, otherwise, the Hadamard gate is applied.

qfunc main(output x: qbit, output ctrl: qbit[]) {
  allocate(2, ctrl);
  hadamard_transform(ctrl);
  allocate(1, x);
  control (ctrl) {
    X(x);
  } else {
    H(x);
  }
}

from classiq import *


@qfunc
def main(x: Output[QBit], ctrl: Output[QArray[QBit]]):
    allocate(2, ctrl)
    hadamard_transform(ctrl)
    allocate(1, x)
    control(ctrl, lambda: X(x), lambda: H(x))

Synthesizing this model creates the following quantum program. Note how the else block is implemented as a negation of the control condition, and the negation is uncomputed after the control operation of the else block.

control_else.jpg