Swap Test Algorithm

View on GitHub Experiment in the IDE

The swap test is a quantum function that checks the overlap between two quantum states. The inputs of the function are two quantum registers of the same size, \(|\psi_1\rangle, \,|\psi_2\rangle\), and it returns as output a single test qubit whose state encodes the overlap between the two inputs: \(|q\rangle_{\rm test} = \alpha|0\rangle + \sqrt{1-\alpha^2}|1\rangle\), with

\[\alpha^2 = \frac{1}{2}\left(1+|\langle \psi_1 |\psi_2 \rangle |^2\right).\]

Thus, the probability of measuring the test qubit at state \(|0\rangle\) is \(1\) if the states are identical (up to a global phase) and 0.5 if the states are orthogonal to each other.

The quantum model starts with an \(H\) gate on the test qubit, followed by swapping between the two states controlled on the test qubit (a controlled-SWAP gate for each of the qubits in the two states) and a final \(H\) gate on the test qubit.

A general scheme of the swap test algorithm:

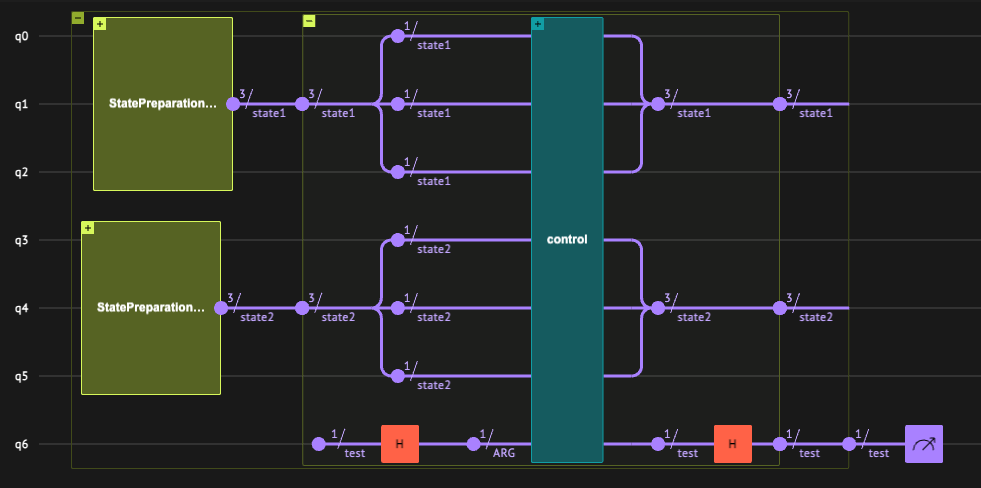
Prepare two random states:

import numpy as np

np.random.seed(12)

NUM_QUBITS = 3
amps1 = 1 - 2 * np.random.rand(
    2**NUM_QUBITS
)  # vector of 2^3 numbers in the range [-1,1]
amps2 = 1 - 2 * np.random.rand(2**NUM_QUBITS)
amps1 = amps1 / np.linalg.norm(amps1)  # normalize the vector
amps2 = amps2 / np.linalg.norm(amps2)

Create a model and synthesize:

from classiq import *


@qfunc
def main(test: Output[QBit]):
    state1 = QArray("state1")
    state2 = QArray("state2")
    prepare_amplitudes(amps1.tolist(), 0.0, state1)
    prepare_amplitudes(amps2.tolist(), 0.0, state2)
    swap_test(state1, state2, test)


qmod = create_model(main)
qmod = set_execution_preferences(qmod, num_shots=100_000)
write_qmod(qmod, "swap_test", decimal_precision=15)
qprog = synthesize(qmod)
show(qprog)

Opening: https://platform.classiq.io/circuit/2sDZTfkLYOewJWOLqSzQB7pgqMW?version=0.66.0

Swap Test Qmod Implementations

The swap test is defined as a library function in the Qmod language. The definition is in the public GitHub. You can add your own functions.

Verify the results:

result = execute(qprog).result_value()

Comparing Measured with Exact Overlap

Using the expected probability of measuring the state \(|0\rangle\) as defined above,

\[\alpha^2 = \frac{1}{2}\left(1+|\langle \psi_1 |\psi_2 \rangle |^2\right),\]

we extract the overlap \(|\langle \psi_1 |\psi_2 \rangle |=\sqrt{2 P\left(q_{\text{test}}=|0\rangle\right)-1}\). The exact overlap is computed with the dot product of the two state vectors. Note that for the sake of this demonstration we execute this circuit \(100,000\) times to improve the precision of the probability estimate. This is usually not required in actual programs.

overlap_from_swap_test = np.sqrt(
    2 * result.counts["0"] / sum(result.counts.values()) - 1
)
exact_overlap = np.abs(amps1 @ amps2)

print("States overlap from Swap-Test result:", overlap_from_swap_test)
print("States overlap from classical calculation:", exact_overlap)

States overlap from Swap-Test result: 0.4673970474874655
States overlap from classical calculation: 0.46972037234759095

RTOL = 0.05
assert np.isclose(
    overlap_from_swap_test, exact_overlap, RTOL
), f"""
The quantum result is too far from the classical one by a relative tolerance of {RTOL}. Please verify your parameters"""