Integer Linear Programming
Introduction
In Integer Linear Programming (ILP), we seek to find a vector of integer numbers that maximizes (or minimizes) a linear cost function under a set of linear equality or inequality constraints [1]. In other words, it is an optimization problem where the cost function to be optimized and all the constraints are linear and the decision variables are integer.
Mathematical Formulation
The ILP problem can be formulated as follows:
Given an \(n\)-dimensional vector \(\vec{c} = (c_1, c_2, \ldots, c_n)\), an \(m \times n\) matrix \(A = (a_{ij})\) with \(i=1,\ldots,m\) and \(j=1,\ldots,n\), and an \(m\)-dimensional vector \(\vec{b} = (b_1, b_2, \ldots, b_m)\), find an \(n\)-dimensional vector \(\vec{x} = (x_1, x_2, \ldots, x_n)\) with integer entries that maximizes (or minimizes) the cost function:
subject to the constraints:
Solving with the Classiq platform
We go through the steps of solving the problem with the Classiq platform, using QAOA algorithm [2]. The solution is based on defining a Pyomo model for the optimization problem we would like to solve.
Building the Pyomo model from a graph input
We proceed by defining the Pyomo model that will be used on the Classiq platform, using the mathematical formulation defined above:
import numpy as np
import pyomo.core as pyo
def ilp(a: np.ndarray, b: np.ndarray, c: np.ndarray, bound: int) -> pyo.ConcreteModel:
# model constraint: a*x <= b
model = pyo.ConcreteModel()
assert b.ndim == c.ndim == 1
num_vars = len(c)
num_constraints = len(b)
assert a.shape == (num_constraints, num_vars)
model.x = pyo.Var(
# here we bound x to be from 0 to to a given bound
range(num_vars),
domain=pyo.NonNegativeIntegers,
bounds=(0, bound),
)
@model.Constraint(range(num_constraints))
def monotone_rule(model, idx):
return a[idx, :] @ list(model.x.values()) <= float(b[idx])
# model objective: max(c * x)
model.cost = pyo.Objective(expr=c @ list(model.x.values()), sense=pyo.maximize)
return model
A = np.array([[1, 1, 1], [2, 2, 2], [3, 3, 3]])
b = np.array([1, 2, 3])
c = np.array([1, 2, 3])
# Instantiate the model
ilp_model = ilp(A, b, c, 3)
ilp_model.pprint()
2 Set Declarations
monotone_rule_index : Size=1, Index=None, Ordered=Insertion
Key : Dimen : Domain : Size : Members
None : 1 : Any : 3 : {0, 1, 2}
x_index : Size=1, Index=None, Ordered=Insertion
Key : Dimen : Domain : Size : Members
None : 1 : Any : 3 : {0, 1, 2}
1 Var Declarations
x : Size=3, Index=x_index
Key : Lower : Value : Upper : Fixed : Stale : Domain
0 : 0 : None : 3 : False : True : NonNegativeIntegers
1 : 0 : None : 3 : False : True : NonNegativeIntegers
2 : 0 : None : 3 : False : True : NonNegativeIntegers
1 Objective Declarations
cost : Size=1, Index=None, Active=True
Key : Active : Sense : Expression
None : True : maximize : x[0] + 2*x[1] + 3*x[2]
1 Constraint Declarations
monotone_rule : Size=3, Index=monotone_rule_index, Active=True
Key : Lower : Body : Upper : Active
0 : -Inf : x[0] + x[1] + x[2] : 1.0 : True
1 : -Inf : 2*x[0] + 2*x[1] + 2*x[2] : 2.0 : True
2 : -Inf : 3*x[0] + 3*x[1] + 3*x[2] : 3.0 : True
5 Declarations: x_index x monotone_rule_index monotone_rule cost
Setting Up the Classiq Problem Instance
In order to solve the Pyomo model defined above, we use the CombinatorialProblem quantum object. Under the hood it tranlates the Pyomo model to a quantum model of the QAOA algorithm, with cost hamiltonian translated from the Pyomo model. We can choose the number of layers for the QAOA ansatz using the argument num_layers, and the penalty_factor, which will be the coefficient of the constraints term in the cost hamiltonian.
from classiq import *
from classiq.applications.combinatorial_optimization import CombinatorialProblem
combi = CombinatorialProblem(pyo_model=ilp_model, num_layers=3, penalty_factor=10)
qmod = combi.get_model()
write_qmod(qmod, "integer_linear_programming")
Synthesizing the QAOA Circuit and Solving the Problem
We can now synthesize and view the QAOA circuit (ansatz) used to solve the optimization problem:
qprog = combi.get_qprog()
show(qprog)
Opening: https://nightly.platform.classiq.io/circuit/2d391a9b-4f75-4b90-ba76-fe6eb0cc3dec?version=0.63.0.dev2
We also set the quantum backend we want to execute on:
from classiq.execution import *
execution_preferences = ExecutionPreferences(
backend_preferences=ClassiqBackendPreferences(backend_name="simulator"),
)
We now solve the problem by calling the optimize method of the CombinatorialProblem object. For the classical optimization part of the QAOA algorithm we define the maximum number of classical iterations (maxiter) and the \(\alpha\)-parameter (quantile) for running CVaR-QAOA, an improved variation of the QAOA algorithm [3]:
optimized_params = combi.optimize(execution_preferences, maxiter=90, quantile=0.7)
Optimization Progress: 76%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 68/90 [02:24<00:46, 2.12s/it]
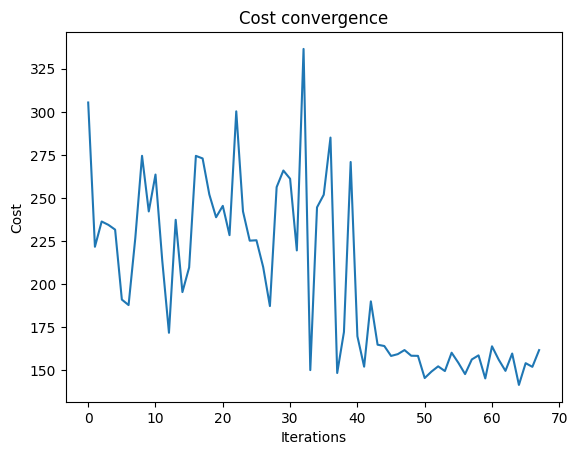
We can check the convergence of the run:
import matplotlib.pyplot as plt
plt.plot(combi.cost_trace)
plt.xlabel("Iterations")
plt.ylabel("Cost")
plt.title("Cost convergence")
Text(0.5, 1.0, 'Cost convergence')
Optimization Results
We can also examine the statistics of the algorithm. The optimization is always defined as a minimzation problem, so the positive maximization objective was tranlated to a negative minimization one by the Pyomo to qmod translator.
In order to get samples with the optimized parameters, we call the sample method:
optimization_result = combi.sample(optimized_params)
optimization_result.sort_values(by="cost").head(5)
| solution | probability | cost | |
|---|---|---|---|
| 18 | {'x': [0, 0, 1], 'monotone_rule_1_slack_var': ... | 0.011719 | -3.000000e+00 |
| 0 | {'x': [0, 1, 0], 'monotone_rule_1_slack_var': ... | 0.030762 | -2.000000e+00 |
| 9 | {'x': [0, 0, 0], 'monotone_rule_1_slack_var': ... | 0.018066 | 1.527468e-150 |
| 150 | {'x': [0, 0, 1], 'monotone_rule_1_slack_var': ... | 0.001465 | 7.000000e+00 |
| 130 | {'x': [0, 1, 0], 'monotone_rule_1_slack_var': ... | 0.001953 | 8.000000e+00 |
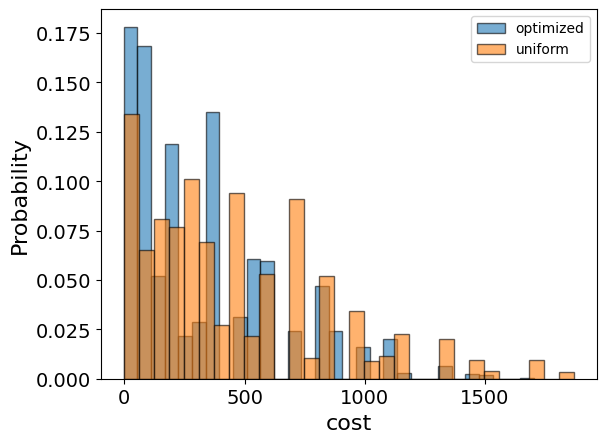
We will also want to compare the optimized results to uniformly sampled results:
uniform_result = combi.sample_uniform()
And compare the histograms:
optimization_result["cost"].plot(
kind="hist",
bins=30,
edgecolor="black",
weights=optimization_result["probability"],
alpha=0.6,
label="optimized",
)
uniform_result["cost"].plot(
kind="hist",
bins=30,
edgecolor="black",
weights=uniform_result["probability"],
alpha=0.6,
label="uniform",
)
plt.legend()
plt.ylabel("Probability", fontsize=16)
plt.xlabel("cost", fontsize=16)
plt.tick_params(axis="both", labelsize=14)
Let us plot the solution:
best_solution = optimization_result.solution[optimization_result.cost.idxmin()]
best_solution
{'x': [0, 0, 1],
'monotone_rule_1_slack_var': [0],
'monotone_rule_2_slack_var': [0]}
Comparison to a classical solver
Lastly, we can compare to the classical solution of the problem:
from pyomo.opt import SolverFactory
solver = SolverFactory("couenne")
solver.solve(ilp_model)
classical_solution = [int(pyo.value(ilp_model.x[i])) for i in range(len(ilp_model.x))]
print("Classical solution:", classical_solution)
Classical solution: [0, 0, 1]
References
[1]: Integer Programming (Wikipedia).
[2]: Farhi, Edward, Jeffrey Goldstone, and Sam Gutmann. "A quantum approximate optimization algorithm." arXiv preprint arXiv:1411.4028 (2014).
[3]: Barkoutsos, Panagiotis Kl, et al. "Improving variational quantum optimization using CVaR." Quantum 4 (2020): 256.