Grover from functional building blocks
Setting the scene
# !pip install -U classiq
new_classiq_user = False
if new_classiq_user:
import classiq
classiq.authenticate()
Warm Up
First Example
Write a function that prepares the minus state \(|{-}\rangle=\frac{1}{\sqrt2}(|{0}\rangle-|{1}\rangle)\), assuming it recives the qubit \(|{x}\rangle=|{0}\rangle\)
HINT
Use H(x),X(x)
from classiq import *
@qfunc
def prepare_minus_state(x: QBit):
pass
# TODO complete here
Now we will test our code:
@qfunc
def main(x: Output[QBit]):
allocate(1, x)
prepare_minus_state(x) # Prepare the minus state
qprog = synthesize(main)
show(qprog)
Quantum program link: https://platform.classiq.io/circuit/2yjA2tiLZD0kptA5ufekX5I4Gil
Some basic explanations about the high-level functional design with Classiq:
-
There should always be a main (
def main(...)) function - the model that captures your algortihm is described there -
The model is always generated out of the main function
-
The model is sent to the synthesis engine (compiler) that return a quantum program which contains the quantum circuit
Some basic guidelines about the modeling language (QMOD):
-
Every quantum variable should be declared, either as a parameter of a funciton e.g.
def prepare_minus(x: QBit)or within the function itself withx = QBit('x') -
Some quantum variables need to be initalized with the
allocatefunction. This is required in 2 cases: -
A variable is a parameter of a function with the declaration
Outputlikedef main(x: Output[QNum]) -
A variable that was declared within a function like
a = QNum('a') -
For the
mainfunction, you will always useOutputfor all variables, as the function does not receive any input
Important tip!
You can see all the declarations of the functions with what are their input arguments in the functions.py file within the classiq package (or by just right clicking a function and presing Go To Defintion)
Uniform Superposition
Let's continue warming up with creating a function that receives a quantum register and creates a uniform superposition for all qubits within this array. You should use the function apply_to_all(gate_operand=, target=):
@qfunc
def create_initial_state(reg: QArray):
pass
# TODO complete here apply_to_all(gate_operand=, target=)
Test yout function by creating a new main function, synthesizing and viewing the circuit:
@qfunc
def main(x: Output[QArray]):
allocate(7, x)
create_initial_state(x)
qprog = synthesize(main)
show(qprog)
Quantum program link: https://platform.classiq.io/circuit/2yjA3FxJAIoqaq58u2aQbECoUar
Function of a function
In our Grover example we will have 3 variables a,b,c. We want to prepare all of them in an initial state of equal superposition. Create a fucntion that receives these 3 quantum variables as quantum integers (QNum) and applies the create_inital_state function to each:
@qfunc
def create_initial_states(a: QNum, b: QNum, c: QNum):
pass
# TODO Complete here
You can create a main function, synthesize and visualize the generated circuit if you want to test yourself.
Oracle - Reflection around bad states
Theoretical Background
Overall we can understand the Grover operator as composed of two reflection operators:
-
Around the superposition of 'bad states' (i.e. not the solutions)
-
Around the initial guess state
In this section we will build the first reflection operator which is also the implementation of the oracle function. Geometrically it can be understood in the 2D vector space of \(\text{Span}\{|{\psi_{\text{good}}}\rangle,|{\psi_{\text{bad}}}\rangle\}\).
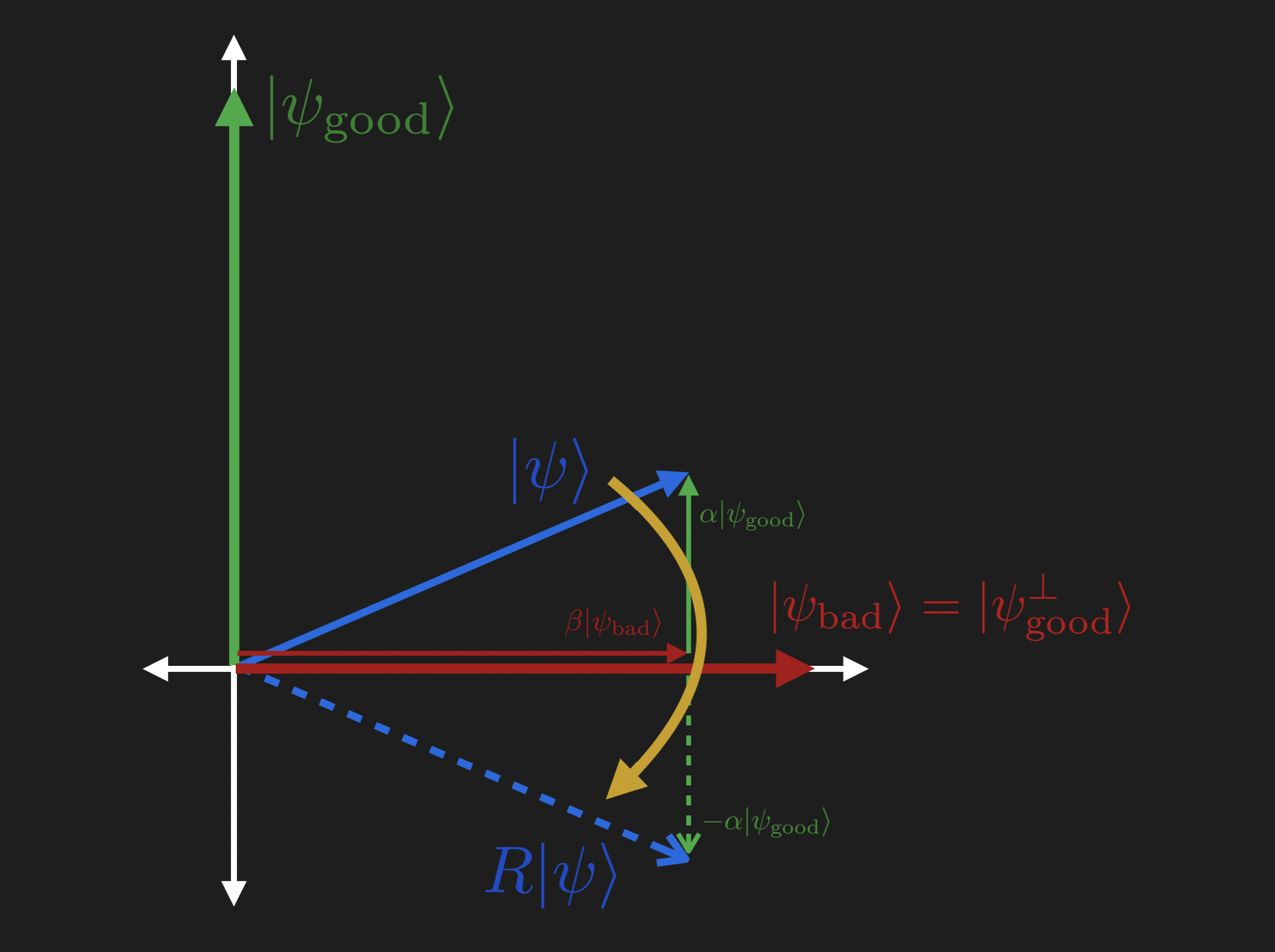
The above figures describes geometrically the reflection of some state \(|{\psi}\rangle=\alpha|{\psi_\text{good}}\rangle+\beta|{\psi_\text{bad}}\rangle\) around the state \(|{\psi_\text{bad}}\rangle\) such that \(\begin{equation} R(\alpha|{\psi_\text{good}}\rangle+\beta|{\psi_\text{bad}}\rangle) = -\alpha|{\psi_\text{good}}\rangle+\beta|{\psi_\text{bad}}\rangle \end{equation}\)
This operator can also be written as \(\begin{equation} R|{x}\rangle=(-1)^{(x==\text{good solution})}|{x}\rangle \end{equation}\)
so if the state of \(x\) is a solution it gets a \((-)\) phase.
Implementation
Now we will actually implement the black box, the oracle, that people are speaking about in quantum algorithms. The beauty of Classiq is that we just need to specify its functionality, and Classiq automatically implements it for us. For our purposes, we want to find all the states that obey \(2a+b=c\) so there are 3 quantum variables. In addition, we want to store our results somewhere, i.e. to indicate for each tupple of 3 numbers (a,b,c) (e.g. (1,2,2)) if the state is what we are looking for (\(2*1+2=4!=2\) so the result is FALSE in this case).
We will store the result in the variable res such that: \(\begin{equation} \text{res} = \text{res} \oplus (2a+b==c) \end{equation}\)
What we really want to implement here is graphically described as:
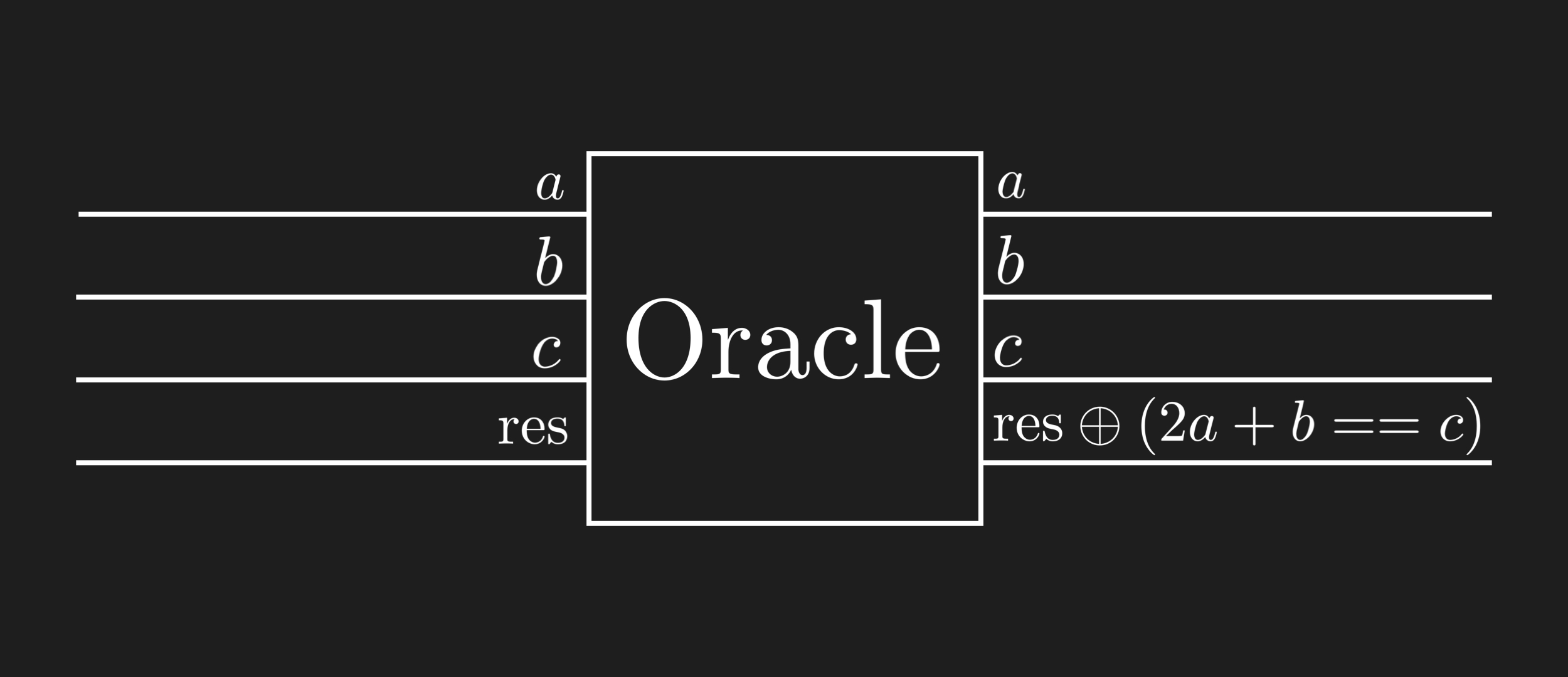
Adapt the following function so it will apply the desired equation:
@qfunc
def oracle_black_box(
res: Permutable[QNum], a: Const[QNum], b: Const[QNum], c: Const[QNum]
):
# TODO Adapt with the correct statement
res ^= a + b + c == 8
Now let's go quantum! We want to store the result of the above operation in the phase of the state \(|{a,b,c}\rangle\). That is, we want \(\begin{equation} |{a,b,c}\rangle\rightarrow(-1)^{(2a+b==c)}|{a,b,c}\rangle\end{equation}\)
There is a common procedure in quantum algorithms that applies this and it is called phase kickback. It's working by applying the above oracle_black_box function to an initial res qubit to the state \(|{-}\rangle\) (has anyone prepared a function prepare_minus(x) by any chance?)
You can work out the math to see that the following scheme implements what we want:

Now we can implement it using our oracle:
@qfunc
def oracle_function(a: Const[QNum], b: Const[QNum], c: Const[QNum]):
aux = QBit()
allocate(aux)
prepare_minus_state(aux)
oracle_black_box(aux, a, b, c)
# We want to bring the aux state back to it's initial value and to free it up for further use
invert(lambda: prepare_minus_state(aux))
free(aux) # and that it can be re-used
Diffuser - Reflection around initial guess
Theoretical Background
The second part of the Grover operator is the diffuser, which can be viewed as the reflection operator around our initial guess.
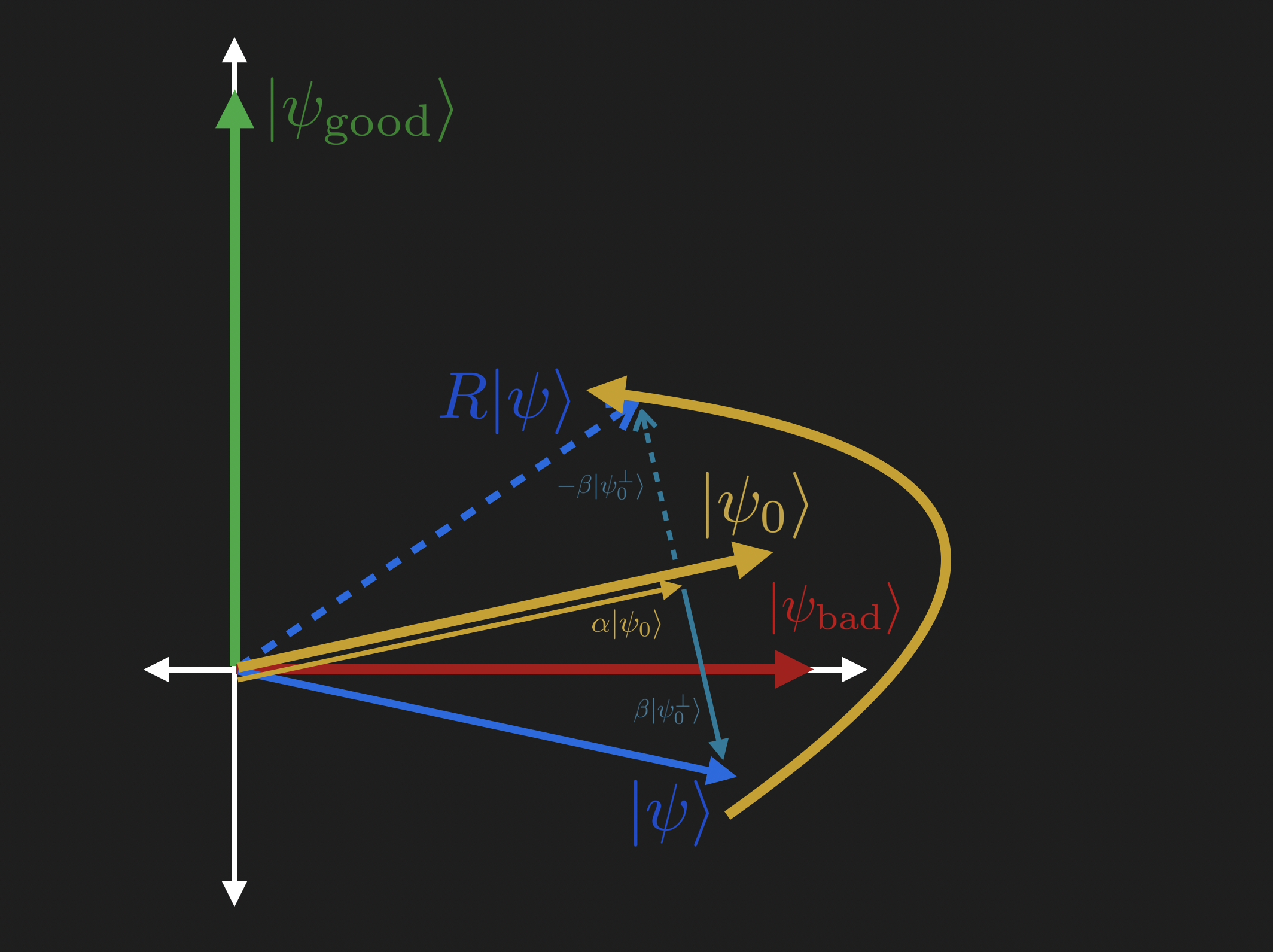
As with the oracle reflection operator, we can describe any state \(|{\psi}\rangle\) as a superposition of the initial state \(|{\psi_0}\rangle\) such that and the orthogoanl state to it \(|{\psi_0^{\bot}}\rangle\)
\(\begin{equation} |{\psi}\rangle = \alpha |{\psi_0}\rangle +\beta |{\psi_0^{\bot}}\rangle \end{equation}\)
Here what we want to implement is to add a \((-)\) phase for all states that are not equal our initial guess, that is the reflection operator (our diffuser) is defined as:
\(\begin{equation} R(\alpha |{\psi_0}\rangle +\beta |{\psi_0^{\bot}}\rangle) = \alpha |{\psi_0}\rangle -\beta |{\psi_0^{\bot}}\rangle \end{equation}\)
In order to implement the reflection around our initial state, we will implement a reflection around the zero state \(|{0}\rangle\), and then squeeze it between to state preperations operators for our initial state \(|{\psi_0}\rangle\). That is, if \(U_{\psi_0}|{0}\rangle=|{\psi_0}\rangle\) then we will implement the desired \(R\) operator with: \(\begin{equation} R = U_{\psi_0}R_0 U_{\psi_0}^{\dagger} \end{equation}\)
where \(R_0\) is the reflection operator around the zero state: \(\begin{equation} R_0|{x}\rangle = (-1)^{(x\ne0)}|{x}\rangle= (2|{0}\rangle\langle{0}|-I)|{x}\rangle \end{equation}\)
Implementation
First we will implement the not equal zero function which takes aux and x as inputs and applies
\(\begin{equation}
\text{res} = \text{res} \oplus (x\ne0)
\end{equation}\)
@qfunc
def not_equal_zero(aux: Permutable[QBit], x: Const[QNum]):
aux ^= x == 0
X(aux)
Now we will use the common trick of phase kick back again. As the aux qubit for the not_equal_zero funciton we need to insert the \(|{-}\rangle\) state after it has been initialized and apploied, and after the application of the function we need to return aux to its initial state and to free it up (We did this precedure before).
HINT
-
Declare the auxilary qubit
-
Initalize it using
allocate -
Prepare the \(|{-}\rangle\) state
-
Apply the
not_equal_zerofunciton -
Reverse the \(|{-}\rangle\) with the
invertoperation -
Free the auxilary qubit
@qfunc
def zero_diffuser(x: QNum):
pass
# TODO complete here
Now after we've implemented the zero diffuser, we need to sandwich it with the state preparations of our initial state a,b,c. The tricky part here is that the zero diffuser expects to receive only 1 quantunm variable x but we have three. So what should we do? We combine them to one quantum variable with the bind operation, treating them as one variable, and then splitting them back into 3 variables with the bind operation again.
size_a = 2
size_b = 2
size_c = 3
@qfunc
def initial_state_diffuser(a: QNum, b: QNum, c: QNum):
create_initial_states(a, b, c)
abc = QNum()
bind([a, b, c], abc)
zero_diffuser(abc)
bind(abc, [a, b, c])
invert(lambda: create_initial_states(a, b, c))
Putting all together
That's it! You've made it! Now is the time to harvest the fruits of the hard work and put everything together!
Complete your grover operator by implementing the two functions that you've built, first the oracle_fucntion and then the inital_state_diffuser:
@qfunc
def my_grover_operator(a: QNum, b: QNum, c: QNum):
# TODO complete here
pass
Now that we have our Grover operator, we can run it within our code. We have 3 steps here:
-
Initalize
a,bandcwithin the scope of themainfunction using theallocateoperation -
Create the initial states for
a,bandc -
Apply your Grover operator
@qfunc
def main(a: Output[QNum], b: Output[QNum], c: Output[QNum]):
allocate(size_a, a)
allocate(size_b, b)
allocate(size_c, c)
# TODO complete here
pass
Synthesize your model:
qprog = synthesize(main)
And view it within the IDE:
show(qprog)
Is it what you were expecting? Now we can play with the constraints as we did in the IDE:
qprog = synthesize(
main, constraints=Constraints(optimization_parameter="depth")
) # or 'width'
show(qprog)
CONGRATULATIONS!
You have completed your own Grover algorithm implementation from functional building blocks without sweeping under the rug any details, really impressive work!
The full solution for your reference
from classiq import *
@qfunc
def prepare_minus_state(x: QBit):
X(x)
H(x)
@qfunc
def create_initial_state(reg: QArray):
apply_to_all(gate_operand=H, target=reg)
@qfunc
def create_initial_state(reg: QArray):
apply_to_all(lambda qb: H(qb), reg)
@qfunc
def create_initial_states(a: QNum, b: QNum, c: QNum):
create_initial_state(a)
create_initial_state(b)
create_initial_state(c)
@qfunc
def oracle_black_box(
res: Permutable[QNum], a: Const[QNum], b: Const[QNum], c: Const[QNum]
):
res ^= 2 * a + b == c
@qfunc
def oracle_function(a: Const[QNum], b: Const[QNum], c: Const[QNum]):
aux = QBit()
allocate(aux)
prepare_minus_state(aux)
oracle_black_box(aux, a, b, c)
# We want to bring the aux state back to it's initial value and to free it up for further use
invert(lambda: prepare_minus_state(aux))
free(aux) # and that it can be re-used
@qfunc
def not_equal_zero(aux: Permutable[QBit], x: Const[QNum]):
aux ^= x == 0
X(aux)
@qfunc
def zero_diffuser(x: QNum):
aux = QBit()
allocate(aux)
prepare_minus_state(aux)
not_equal_zero(aux, x)
invert(lambda: prepare_minus_state(aux))
free(aux)
size_a = 2
size_b = 2
size_c = 3
@qfunc
def initial_state_diffuser(a: QNum, b: QNum, c: QNum):
create_initial_states(a, b, c)
abc = QNum()
bind([a, b, c], abc)
zero_diffuser(abc)
bind(abc, [a, b, c])
invert(lambda: create_initial_states(a, b, c))
@qfunc
def my_grover_operator(a: QNum, b: QNum, c: QNum):
oracle_function(a, b, c)
initial_state_diffuser(a, b, c)
@qfunc
def main(a: Output[QNum], b: Output[QNum], c: Output[QNum]):
allocate(size_a, a)
allocate(size_b, b)
allocate(size_c, c)
create_initial_states(a, b, c)
my_grover_operator(a, b, c)
qmod = create_model(main)
qprog = synthesize(main)
show(qprog)
qmod = set_constraints(qmod, optimization_parameter="depth") # or 'width'
qprog = synthesize(qmod)
show(qprog)
write_qmod(qmod, "grover_workshop")