Facility Location Problem (P-median)
We consider the following optimization problem: we have a set of \(M\) customers and a set of \(N\) potential locations for opening a facility. Given transportation costs between facilities and customers and how many facilities we would like to open (\(P\)), we need to determine which facilities to open such that the total transportation cost between facilities and customers is minimal, under the constraint that each customer is allocated to only one facility.
Possible extensions:
\(\bullet\) Add different demand for each customer.
\(\bullet\) Add cost for opening a facility at each location.
\(\bullet\) Different categories of facilities, and customer can have multiple allocations for different facilities.
Mathematical Modeling
The input of the model is a set of \(M\) customers \(\{1,\dots,M\}\), a set of \(N\) potential locations for facilities \(\{1,\dots,N\}\), an \(N\times M\) matrix \(d\) where \(d_{nm}\) is the cost of customer \(m\) buying from facility \(n\), and the total number of facilities we want to open \(P\).
We define a binary variable for the optimization problem: an \(N\times M\) matrix \(x\) such that \(x_{nm}=1\) if customer \(m\) is allocated to facility \(n\).
The objective function to minimize is the total cost function:
We have 2 constraints:
(1) Each customer is supplied: \(\forall m\in[0,M] \,\,\, \sum_n x_{nm}=1\).
(2) Total number of opened facilities is \(P\): \(\sum_n\Pi_m (1-x_{nm})=N-P\) (The inner product is zero if the \(n-\)th facility is not open).
Alternative modeling
We note that there is an alternative modeling, in which one adds another variable to the model: a binary vector \(y\) of size \(N\) which indicates which facilities are open. In this formulation the second constraint can be written as \(\sum_n y_n=P\) together with an inequality constraint \(\forall n,m:\, x_{nm} \leq y_n\). A model which combines equality and inequality constraints will be available in the future.
Note that in this alternative modeling we have a QUBO problem (compared to the formulation above where constraint (2) is polynomial of degree \(m\)). However, the alternative modelling has more variables to minimize on, and thus refers to more qubits.
An Example
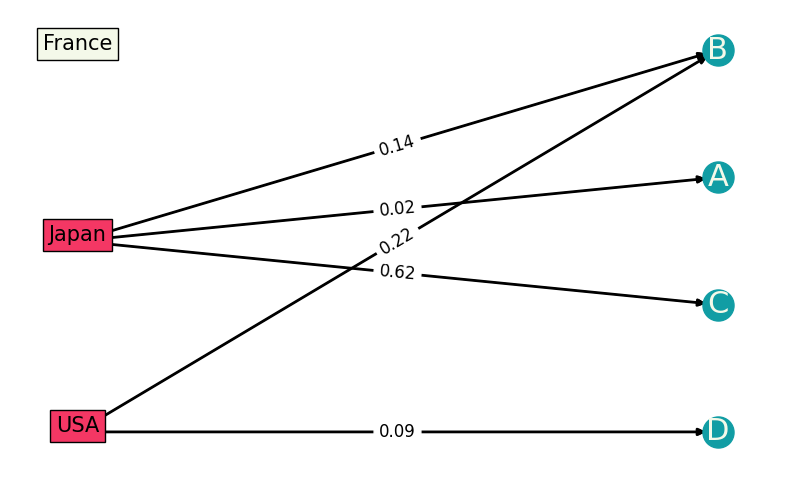
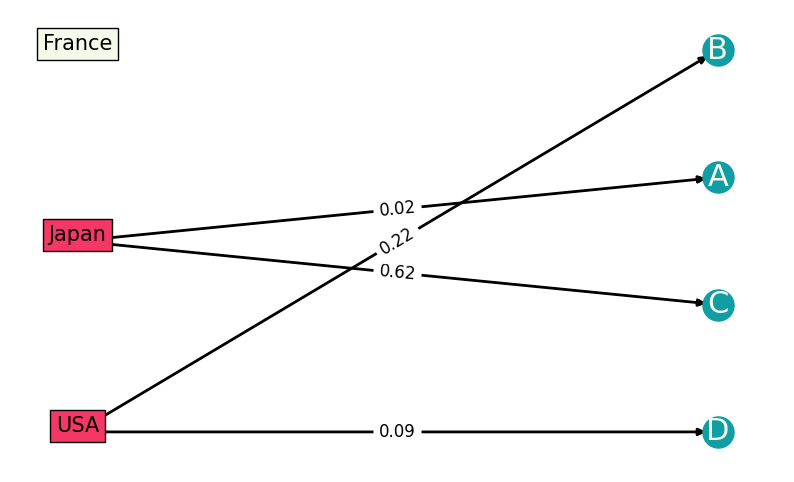
Let us say we can open facilities in Japan, USA, and France, and we have 4 customers whose costs for buying from these three locations are given. We would like to open in total \(P=2\) facilities. The optimization problem is to find where to open the facilities and which customer is allocated to which facility.
We now draw this specific example on a graph. We have \(N=3\) locations and \(M=4\) customers, where the weights of the edges between them signify the costs:
Suggestions:
-
Give general problem description and then givens, or provide givens after each mention.
-
Standardize writing numbers appearing in sentences out when less than 10. "4" vs "four".
# Import relevant packages
from itertools import product
import matplotlib.pyplot as plt
import networkx as nx # noqa
import numpy as np
import pandas as pd
# Declare givens from problem statement
Facilities = ["Japan", "USA", "France"]
Customers = ["A", "B", "C", "D"]
N = len(Facilities) # potential facility count
M = len(Customers) # customer count
P = 2 # allocated facility count
# costs of customers using facilities
d = np.array(
[[0.02, 0.14, 0.62, 0.11], [0.99, 0.22, 0.91, 0.09], [0.4, 0.76, 0.95, 0.61]]
)
graph = nx.DiGraph()
graph.add_nodes_from(Facilities + Customers)
for n, m in product(range(N), range(M)):
graph.add_edges_from([(Facilities[n], Customers[m])], weight=d[n, m])
# Plot the graph
plt.figure(figsize=(10, 6))
left = nx.bipartite.sets(graph)[0]
pos = nx.bipartite_layout(graph, left)
nx.draw_networkx(graph, pos=pos, nodelist=Customers, font_size=22, font_color="None")
nx.draw_networkx_nodes(
graph, pos, nodelist=Customers, node_color="#119DA4", node_size=500
)
for fa in Facilities:
x, y = pos[fa]
plt.text(
x,
y,
s=fa,
bbox=dict(facecolor="#F43764", alpha=1),
horizontalalignment="center",
fontsize=15,
)
nx.draw_networkx_edges(graph, pos, width=2)
labels = nx.get_edge_attributes(graph, "weight")
nx.draw_networkx_edge_labels(graph, pos, edge_labels=labels, font_size=12)
nx.draw_networkx_labels(
graph,
pos,
labels={co: co for co in Customers},
font_size=22,
font_color="#F4F9E9",
)
plt.axis("off")
plt.show()
Building the Pyomo model from a matrix of distances input
from typing import List, Tuple, cast # noqa
import pyomo.environ as pyo
from IPython.display import Markdown, display
## We define a function which gets a matrix of costs between customers and potential facilities
## and the number of facilities to open.
def pmedian(cost_mat: np.ndarray, P: int) -> pyo.ConcreteModel:
model = pyo.ConcreteModel("pmedian")
N = cost_mat.shape[0] # potential facility amount
M = cost_mat.shape[1] # customer count
Locations = range(N)
Customers = range(M)
model.x = pyo.Var(Locations, Customers, domain=pyo.Binary)
@model.Constraint(Customers)
def each_customer_is_supplied_rule(model, m): # constraint (1)
return sum(model.x[n, m] for n in Locations) == 1
def is_location_alocated(n): # constraint (2)
return np.prod([(1 - model.x[n, m]) for m in Customers])
model.num_facilities = pyo.Constraint(
expr=sum(is_location_alocated(n) for n in Locations) == N - P
)
model.cost = pyo.Objective(
expr=sum(cost_mat[n, m] * model.x[n, m] for n in Locations for m in Customers),
sense=pyo.minimize,
)
return model
Solving with Classiq
We take a specific example: the one outlined above
pmedian_model = pmedian(d, P)
from classiq import construct_combinatorial_optimization_model
from classiq.applications.combinatorial_optimization import OptimizerConfig, QAOAConfig
qaoa_config = QAOAConfig(num_layers=5, penalty_energy=10)
For the classical optimization part of the QAOA algorithm (CombinatorialConfig) we define the maximum number of classical iterations (max_iteration) and the \(\alpha\)-parameter (alpha_cvar) for running CVaR-QAOA, an improved variation of the QAOA algorithm [3]:
optimizer_config = OptimizerConfig(
max_iteration=30,
alpha_cvar=1,
)
Lastly, we define the CombinatorialOptimization instance which we can use to solve the problem:
qmod = construct_combinatorial_optimization_model(
pyo_model=pmedian_model,
qaoa_config=qaoa_config,
optimizer_config=optimizer_config,
)
We also set the quantum backend we want to execute on:
from classiq import set_execution_preferences
from classiq.execution import ClassiqBackendPreferences, ExecutionPreferences
backend_preferences = ExecutionPreferences(
backend_preferences=ClassiqBackendPreferences(backend_name="simulator")
)
qmod = set_execution_preferences(qmod, backend_preferences)
from classiq import write_qmod
write_qmod(qmod, "facility_location")
We define a function that plot solutions
# This function plots the solution in a table and a graph
def plotting_sol(x_sol, cost, is_classic: bool):
x_sol_to_mat = np.reshape(np.array(x_sol), [N, M]) # vector to matrix
# opened facilities will be marked in red
opened_fac_dict = {}
for fa in range(N):
if sum(x_sol_to_mat[fa, m] for m in range(M)) > 0:
opened_fac_dict.update({Facilities[fa]: "background-color: #F43764"})
# classical or quantum
if is_classic == True:
display(Markdown("**CLASSICAL SOLUTION**"))
print("total cost= ", cost)
else:
display(Markdown("**QAOA SOLUTION**"))
print("total cost= ", cost)
# plotting in a table
df = pd.DataFrame(x_sol_to_mat)
df.columns = Customers
df.index = Facilities
plotable = df.style.apply(lambda x: x.index.map(opened_fac_dict))
display(plotable)
# plotting in a graph
graph_sol = nx.DiGraph()
graph_sol.add_nodes_from(Facilities + Customers)
for n, m in product(range(N), range(M)):
if x_sol_to_mat[n, m] > 0:
graph_sol.add_edges_from([(Facilities[n], Customers[m])], weight=d[n, m])
plt.figure(figsize=(10, 6))
left = nx.bipartite.sets(graph_sol, top_nodes=Facilities)[0]
pos = nx.bipartite_layout(graph_sol, left)
nx.draw_networkx(
graph_sol, pos=pos, nodelist=Customers, font_size=22, font_color="None"
)
nx.draw_networkx_nodes(
graph_sol, pos, nodelist=Customers, node_color="#119DA4", node_size=500
)
for fa in Facilities:
x, y = pos[fa]
if fa in opened_fac_dict.keys():
plt.text(
x,
y,
s=fa,
bbox=dict(facecolor="#F43764", alpha=1),
horizontalalignment="center",
fontsize=15,
)
else:
plt.text(
x,
y,
s=fa,
bbox=dict(facecolor="#F4F9E9", alpha=1),
horizontalalignment="center",
fontsize=15,
)
nx.draw_networkx_edges(graph_sol, pos, width=2)
labels = nx.get_edge_attributes(graph_sol, "weight")
nx.draw_networkx_edge_labels(graph, pos, edge_labels=labels, font_size=12)
nx.draw_networkx_labels(
graph_sol,
pos,
labels={co: co for co in Customers},
font_size=22,
font_color="#F4F9E9",
)
plt.axis("off")
plt.show()
Now we can create a quantum circuit using the synthesize command and show it
from classiq import show, synthesize
qprog = synthesize(qmod)
show(qprog)
Opening: https://platform.classiq.io/circuit/d804bf78-fab4-4ab0-b897-5fddca1b51f2?version=0.41.0.dev39%2B79c8fd0855
We now solve the problem by calling the execute function on the quantum program we have generated:
from classiq import execute
res = execute(qprog).result()
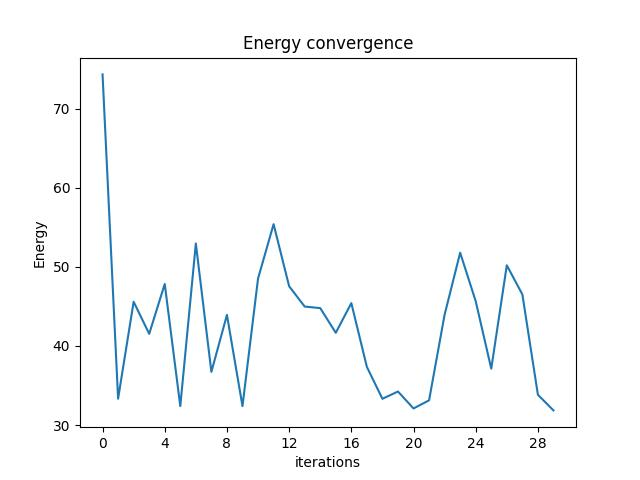
We can check the convergence of the run:
from classiq.execution import VQESolverResult
vqe_result = res[0].value
vqe_result.convergence_graph
Optimizer statistics
import pandas as pd
from classiq.applications.combinatorial_optimization import (
get_optimization_solution_from_pyo,
)
solution = get_optimization_solution_from_pyo(
pmedian_model, vqe_result=vqe_result, penalty_energy=qaoa_config.penalty_energy
)
optimization_result = pd.DataFrame.from_records(solution)
optimization_result.sort_values(by="cost", ascending=True).head(5)
| probability | cost | solution | count | |
|---|---|---|---|---|
| 535 | 0.001 | 0.95 | [1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0] | 1 |
| 504 | 0.001 | 0.97 | [1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0] | 1 |
| 257 | 0.001 | 1.27 | [0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0] | 1 |
| 536 | 0.001 | 1.39 | [1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1] | 1 |
| 35 | 0.004 | 1.51 | [1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0] | 4 |
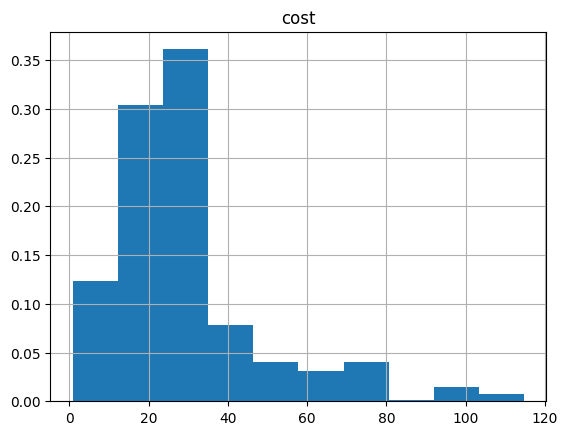
optimization_result.hist("cost", weights=optimization_result["probability"])
array([[<Axes: title={'center': 'cost'}>]], dtype=object)
Best solution
We plot the quantum result only if we get the right solution (to avoid problems with printing table and graph).
best_solution = optimization_result.loc[optimization_result.cost.idxmin()]
plotting_sol(best_solution.solution, best_solution.cost, is_classic=False)
QAOA SOLUTION
total cost= 0.9499999999999922
| A | B | C | D | |
|---|---|---|---|---|
| Japan | 1 | 0 | 1 | 0 |
| USA | 0 | 1 | 0 | 1 |
| France | 0 | 0 | 0 | 0 |
Compare to a classical solver
from pyomo.opt import SolverFactory
solver = SolverFactory("couenne")
solver.solve(pmedian_model)
pmedian_model.display()
Model pmedian
Variables:
x : Size=12, Index=x_index
Key : Lower : Value : Upper : Fixed : Stale : Domain
(0, 0) : 0 : 1.0 : 1 : False : False : Binary
(0, 1) : 0 : 1.0 : 1 : False : False : Binary
(0, 2) : 0 : 1.0 : 1 : False : False : Binary
(0, 3) : 0 : 0.0 : 1 : False : False : Binary
(1, 0) : 0 : 0.0 : 1 : False : False : Binary
(1, 1) : 0 : 6.846989283059948e-10 : 1 : False : False : Binary
(1, 2) : 0 : 0.0 : 1 : False : False : Binary
(1, 3) : 0 : 1.0 : 1 : False : False : Binary
(2, 0) : 0 : 0.0 : 1 : False : False : Binary
(2, 1) : 0 : -6.846989283059948e-10 : 1 : False : False : Binary
(2, 2) : 0 : 0.0 : 1 : False : False : Binary
(2, 3) : 0 : 0.0 : 1 : False : False : Binary
Objectives:
cost : Size=1, Index=None, Active=True
Key : Active : Value
None : True : 0.8699999996302625
Constraints:
each_customer_is_supplied_rule : Size=4
Key : Lower : Body : Upper
0 : 1.0 : 1.0 : 1.0
1 : 1.0 : 1.0 : 1.0
2 : 1.0 : 1.0 : 1.0
3 : 1.0 : 1.0 : 1.0
num_facilities : Size=1
Key : Lower : Body : Upper
None : 1.0 : 1.000000000684699 : 1.0
best_classical_solution = np.array(
[pyo.value(pmedian_model.x[idx]) for idx in np.ndindex(d.shape)]
).reshape(d.shape)
plotting_sol(best_classical_solution, pyo.value(pmedian_model.cost), is_classic=True)
CLASSICAL SOLUTION
total cost= 0.8699999996302625
| A | B | C | D | |
|---|---|---|---|---|
| Japan | 1.000000 | 1.000000 | 1.000000 | 0.000000 |
| USA | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
| France | 0.000000 | -0.000000 | 0.000000 | 0.000000 |
