Qsvm pauli feature map
Generating Qiskit's data
from itertools import combinations
from qiskit_algorithms.utils import algorithm_globals
from qiskit_machine_learning.datasets import ad_hoc_data
from sklearn.svm import SVC
from classiq import *
seed = 12345
algorithm_globals.random_seed = seed
adhoc_dimension = 2
train_features, train_labels, test_features, test_labels, adhoc_total = ad_hoc_data(
training_size=20,
test_size=5 + 5, # 5 for test, 5 for predict
n=adhoc_dimension,
gap=0.3,
plot_data=False,
one_hot=False,
include_sample_total=True,
)
# the `test_features` and `test_labels` are of size which is double that of the `test_size` argument
# Since there are `test_size` items for each `adhoc_dimension`
import numpy as np
def split(obj: np.ndarray, n: int = 20):
quarter = n // 4
half = n // 2
first = np.concatenate((obj[:quarter], obj[half : half + quarter]))
second = np.concatenate((obj[quarter:half], obj[half + quarter :]))
return first, second
test_features, predict_features = split(test_features)
test_labels, predict_labels = split(test_labels)
# Plot data
import matplotlib.pyplot as plt
import numpy as np
plt.figure(figsize=(5, 5))
plt.ylim(0, 2 * np.pi)
plt.xlim(0, 2 * np.pi)
plt.imshow(
np.asmatrix(adhoc_total).T,
interpolation="nearest",
origin="lower",
cmap="RdBu",
extent=[0, 2 * np.pi, 0, 2 * np.pi],
)
plt.scatter(
train_features[np.where(train_labels[:] == 0), 0],
train_features[np.where(train_labels[:] == 0), 1],
marker="s",
facecolors="w",
edgecolors="b",
label="A train",
)
plt.scatter(
train_features[np.where(train_labels[:] == 1), 0],
train_features[np.where(train_labels[:] == 1), 1],
marker="o",
facecolors="w",
edgecolors="r",
label="B train",
)
plt.scatter(
test_features[np.where(test_labels[:] == 0), 0],
test_features[np.where(test_labels[:] == 0), 1],
marker="s",
facecolors="b",
edgecolors="w",
label="A test",
)
plt.scatter(
test_features[np.where(test_labels[:] == 1), 0],
test_features[np.where(test_labels[:] == 1), 1],
marker="o",
facecolors="r",
edgecolors="w",
label="B test",
)
plt.legend(bbox_to_anchor=(1.05, 1), loc="upper left", borderaxespad=0.0)
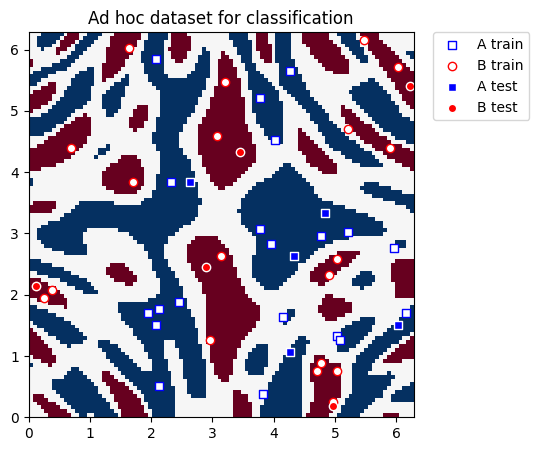
plt.title("Ad hoc dataset for classification")
plt.show()
Building Classiq's QSVM
We build a Pauli feature map. This feature map is of size \(N\) qubits for data \(\vec{x}\) of size \(N\), and it corresponds to the following unitary:
\[U = \left(\hbox{Hadamarad Transform}\right) \exp\left(\sum f^{(1)}_k(\vec{x})H^{(1)}_k + \sum f^{(2)}_k(\vec{x})H^{(2)}_k+\dots \right),\]
where \(H^{(i)}\) is an Hamiltonian acting on \(i\) qubits according to some connectivity map, and \(f^{(i)}\) is some classical function, typically taken as polynomial of degree \(i\). For example, if our data is of size \(3\) and we assume circular connectivity, taking Hamiltonians depending only on \(Z\), the Hamiltonian reads:
\[\sum f^{(1)}_k(\vec{x})H^{(1)}_k = \alpha(x_0+\beta)ZII+\alpha(x_1+\beta)IZI+\alpha(x_2+\beta)IIZ,\]
\[\sum f^{(2)}_k(\vec{x})H^{(2)}_k = \gamma^2(x_0+\zeta)(x_1+\zeta)ZZI+\gamma^2(x_1+\zeta)(x_2+\zeta)IZZ + \gamma^2(x_0+\zeta)(x_3+\zeta)ZIZ,\]
where \((\alpha,\beta)\) and \((\gamma,\zeta)\) define some affine transformation on the data and corresponds to the functions \(f^{(1,2)}\).
We start with defining classical functions for creating a connectivity map for the Hamiltonians and for generating the full Hamiltonian:
from itertools import combinations, islice
import numpy as np
from classiq import *
def generate_connectivity_map(list_size, sublist_size, connectivity_type):
"""
Generate connectivity for a given list size and sublist size.
Parameters:
- list_size: The size of the list (number of elements).
- sublist_size: The size of the subsets to generate.
- connectivity_type: an integer (0 for linear, 1 for circular, 2 for full)
Returns:
- A list of all unique subsets of the given size.
"""
assert connectivity_type in [
0,
1,
2,
], "connectivity must be 0 (linear), 1 (circular), or 2 (full)"
if connectivity_type == 0: # linear
return [
list(range(i, i + sublist_size))
for i in range(list_size - sublist_size + 1)
]
elif connectivity_type == 1: # circular
return [
[(i + j) % list_size for j in range(sublist_size)] for i in range(list_size)
]
elif connectivity_type == 2: # full
return [list(comb) for comb in combinations(range(list_size), sublist_size)]
def generate_hamiltonian(
data: CArray[CReal],
paulis_list: CArray[CArray[Pauli]],
affines: CArray[CArray[CReal, 2]],
connectivity: CInt,
) -> CArray[PauliTerm]:
assert connectivity in [
0,
1,
2,
], "connectivity must be 0 (linear), 1 (circular) or 2 (full)"
ham = []
ham0 = [Pauli.I] * data.len
for paulis, affine in zip(paulis_list, affines):
indices = generate_connectivity_map(data.len, paulis.len, connectivity)
for k in range(len(indices)):
ham_temp = ham0.copy()
coe_temp = 1
for j in range(len(indices[0])):
ham_temp[indices[k][j]] = paulis[j]
coe_temp *= affine[0] * (data[indices[k][j]] - affine[1])
ham += [PauliTerm(pauli=ham_temp, coefficient=coe_temp)]
return ham
Next, we define a quantum function for the Pauli feature map, working in generative mode:
@qfunc(generative=True)
def pauli_kernel(
data: CArray[CReal],
paulis_list: CArray[CArray[Pauli]],
affines: CArray[CArray[CReal, 2]],
connectivity: CInt,
reps: CInt,
qba: QArray[QBit],
) -> None:
power(
reps,
lambda: (
hadamard_transform(qba),
suzuki_trotter(
generate_hamiltonian(data, paulis_list, affines, connectivity),
evolution_coefficient=-1,
order=1,
repetitions=1,
qbv=qba,
),
),
)
Finally, we constuct the quantum model for the QSVM routine:
N_DIM = 2
PAULIS = [[Pauli.Z], [Pauli.Z, Pauli.Z]]
CONNECTIVITY = 2
AFFINES = [[1, 0], [1, np.pi]]
REPS = 2
@qfunc
def main(data1: CArray[CReal, N_DIM], data2: CArray[CReal, N_DIM], qba: Output[QNum]):
allocate(data1.len, qba)
pauli_kernel(data1, PAULIS, AFFINES, CONNECTIVITY, REPS, qba)
invert(lambda: pauli_kernel(data2, PAULIS, AFFINES, CONNECTIVITY, REPS, qba))
QSVM_PAULI_Z_ZZ = create_model(main, out_file="qsvm_pauli_feature_map")
Viewing the model's parameterized quantum circuit:
qprog = synthesize(QSVM_PAULI_Z_ZZ)
show(qprog)
Opening: https://platform.classiq.io/circuit/2rMasNwVKqDT6a17tVqYrGxDj9t?version=0.65.1
Execute QSVM
The first step in QSVM is the training. The second step in QSVM is to test the training process. The last QSVM step, which may be applied multiple times on different datasets, is prediction: the prediction process takes unlabeled data, and returns its predicted labels.
Next, we define classical functions for applying these three parts of execution, where the latter is done via ExecutionSession and batch_sample.
def get_execution_params(data1, data2=None):
"""
Generate execution parameters based on the mode (train or validate).
Parameters:
- data1: First dataset (used for both training and validation).
- data2: Second dataset (only required for validation).
Returns:
- A list of dictionaries with execution parameters.
"""
if data2 is None:
# Training mode (symmetric pairs of data1)
return [
{"data1": data1[k], "data2": data1[j]}
for k in range(len(data1))
for j in range(k, len(data1)) # Avoid symmetric pairs
]
else:
# Prediction mode
return [
{"data1": data1[k], "data2": data2[j]}
for k in range(len(data1))
for j in range(len(data2))
]
def construct_kernel_matrix(matrix_size, res_batch, train=False):
"""
Construct a kernel matrix from `res_batch`, depending on whether it's for training or predicting.
Parameters:
- matrix_size: Tuple of (number of rows, number of columns) for the matrix.
- res_batch: Precomputed batch results.
- train: Boolean flag. If True, assumes training (symmetric matrix).
Returns:
- A kernel matrix as a NumPy array.
"""
rows, cols = matrix_size
kernel_matrix = np.zeros((rows, cols))
num_shots = res_batch[0].num_shots
num_output_qubits = len(next(iter(res_batch[0].counts)))
count = 0
if train: # and rows == cols:
# Symmetric matrix (training)
for k in range(rows):
for j in range(k, cols):
value = (
res_batch[count].counts.get("0" * num_output_qubits, 0) / num_shots
)
kernel_matrix[k, j] = value
kernel_matrix[j, k] = value # Use symmetry
count += 1
else:
# Non-symmetric matrix (validation)
for k in range(rows):
for j in range(cols):
kernel_matrix[k, j] = (
res_batch[count].counts.get("0" * num_output_qubits, 0) / num_shots
)
count += 1
return kernel_matrix
def train_svm(es, train_data, train_labels):
"""
Trains an SVM model using a custom precomputed kernel from the training data.
Parameters:
- es: ExecutionSession object to process batch execution for kernel computation.
- train_data: List of data points for training.
- train_labels: List of binary labels corresponding to the training data.
Returns:
- svm_model: A trained SVM model using the precomputed kernel.
"""
train_size = len(train_data)
train_execution_params = get_execution_params(train_data)
res_train_batch = es.batch_sample(train_execution_params) # execute batch
# generate kernel matrix for train
kernel_train = construct_kernel_matrix(
matrix_size=(train_size, train_size), res_batch=res_train_batch, train=True
)
svm_model = SVC(kernel="precomputed")
svm_model.fit(
kernel_train, train_labels
) # the fit gets the precomputed matrix of training, and the training labels
return svm_model
def predict_svm(es, data, train_data, svm_model):
"""
Predicts labels for new data using a precomputed kernel with a trained SVM model.
Parameters:
- es: ExecutionSession object to process batch execution for kernel computation.
- data (list): List of new data points to predict.
- train_data (list): Original training data used to train the SVM.
- svm_model: A trained SVM model returned by `train_svm`.
Returns:
- y_predict (list): Predicted labels for the input data.
"""
predict_size = len(data)
train_size = len(train_data)
predict_execution_params = get_execution_params(data, train_data)
res_predict_batch = es.batch_sample(predict_execution_params) # execute batch
kernel_predict = construct_kernel_matrix(
matrix_size=(predict_size, train_size), res_batch=res_predict_batch, train=False
)
y_predict = svm_model.predict(
kernel_predict
) # the predict gets the precomputed test matrix
return y_predict
We can now run the execution session with all three parts:
from classiq.execution import ExecutionSession
with ExecutionSession(qprog) as es:
# train
svm_model = train_svm(es, train_features.tolist(), train_labels.tolist())
# test
y_test = predict_svm(es, test_features.tolist(), train_features.tolist(), svm_model)
test_score = sum(y_test == test_labels.tolist()) / len(test_labels.tolist())
# print("quantum kernel classification test score: %0.2f" % (test_score))
# predict
predicted_labels = predict_svm(
es, predict_features.tolist(), train_features.tolist(), svm_model
)
# Printing tests result
print(f"Testing success ratio: {test_score}")
print()
# Printing predictions
print("Prediction from datapoints set:")
print(f" ground truth: {predict_labels}")
print(f" prediction: {predicted_labels}")
print(
f" success rate: {100 * np.count_nonzero(predicted_labels == predict_labels) / len(predicted_labels)}%"
)
Testing success ratio: 1.0
Prediction from datapoints set:
ground truth: [0 0 0 0 0 1 1 1 1 1]
prediction: [0 0 0 0 0 1 1 1 1 1]
success rate: 100.0%