Quantum Counting Using the Iterative Quantum Amplitude Estimation Algorithm
The quantum counting algorithm [1] efficiently estimates the number of valid solutions to a search problem, based on the amplitude estimation algorithm. It demonstrates a quadratic improvement with regard to a classical algorithm with black box oracle access to the function \(f\).
More precisely, given a Boolean function \(f :\{0, 1\}^n\rightarrow\{0,1\}\), the counting problem estimates the number of inputs \(x\) to \(f\) such that \(f(x)=1\).
This tutorial demonstrates how to estimate the counting problem using a specific variant of the amplitude estimation algorithm: the Iterative Quantum Amplitude Estimation (IQAE) [2].
The IQAE does not rely on the Quantum Phase Estimation algorithm [3], but purely on applications of the grover operator:
thereby reducing the required number of qubits and gates of the circuit, at the expense of additional multiplicative factor polylogarithmic in the error \(\epsilon\).
Setting Up the Problem
We choose this equation:
where \(a\), \(b\) are 2-bit unsigned integers. This equation has six solutions. The goal is to estimate the number of valid solutions out of the 16 possible inputs, with precision \(0.5\).
Amplitude Estimation Using Phase Estimation
We first show how to use quantum phase estimation algorithm for quantum counting [3], then solve it using the IQAE method.
Given a state \(|\psi\rangle\) such that \(|\psi\rangle=\sqrt{a}|\psi_1\rangle+\sqrt{1-a}|\psi_0\rangle\) we can measure \(a\) up to arbitrary precision, given the following building blocks: 1) State preparation: A unitary \(A\) such that: \(A|0\rangle = |\psi\rangle = \sqrt{a}|\psi_1\rangle+\sqrt{1-a}|\psi_0\rangle\).
2) Oracle: A unitary \(S_{\psi_1}\) such that \(S_{\psi_1}=I-2|\psi_1\rangle\langle\psi_1|\), which adds a \((-1)\) phase to \(|\psi_1|\psi\rangle\rangle\) and does nothing to any orthognal states to \(|\psi_1\rangle\). This is effectively a reflection around the "good" state \(|\psi_1\rangle\).
Given these two functions, we can construct the Grover operator:
which is exactly the same operator as for the Grover's search algorithm.
In the subspace spanned by \(|\psi_1\rangle\) and \(|\psi_0\rangle\), \(Q\) has two eigenvalues:
Therefore, if we apply a QPE on \(A|0\rangle\) we have these two eigenvalues encoded in the QPE register; however, both give the value of \(a\), so there is no ambiguity.
Arithmetic Oracle
We define the \(S_{\psi_1}\) oracle:
from classiq import *
A_SIZE = 2
B_SIZE = 2
DOMAIN_SIZE = A_SIZE + B_SIZE
class OracleVars(QStruct):
a: QNum[A_SIZE]
b: QNum[B_SIZE]
@qfunc
def arith_equation(state: Const[OracleVars], res: Permutable[QBit]):
res ^= state.a + state.b <= 2
# use phase kickback for turning the arith_equation to an oracle
@qfunc
def arith_oracle(state: OracleVars):
phase_oracle(arith_equation, state)
Diffuser
The diffuser consists of the reflection around the \(|0\rangle\) state and a state-preparation function.
The state preparation function \(A\) reflects knowledge about the solution space and can be used to eliminate invalid assignments. Here we assume no knowledge of the solution space; hence, we use the uniform superposition state preparation.
import numpy as np
@qfunc
def reflection_about_zero(x: QArray[QBit]):
within_apply(
lambda: inplace_xor((2**x.len) - 1, x),
lambda: control(x[0 : x.len - 1], lambda: Z(x[x.len - 1])),
)
@qfunc
def my_diffuser(sp_operand: QCallable[QArray], x: QArray[QBit]):
within_apply(
lambda: invert(lambda: sp_operand(x)),
lambda: reflection_about_zero(x),
)
sp_oracle = lambda x: hadamard_transform(x)
Defining a Complete Grover Operator
@qfunc
def my_grover_operator(
oracle_operand: QCallable[QArray],
sp_operand: QCallable[QArray],
x: QArray[QBit],
):
oracle_operand(x)
my_diffuser(sp_operand, x)
U(0, 0, 0, np.pi, x[0])
Wrapping All to the Phase Estimation
We will achieve the desired precision only in the IQAE phase. Here, we compute the worst-case precision for five phase qubits:
NUM_PHASE_QUBITS = 5
x = np.linspace(0, 1, 100)
(2**DOMAIN_SIZE) * max(
np.abs(
np.sin(np.pi * x) ** 2 - np.sin(np.pi * (x - 1 / (2**NUM_PHASE_QUBITS))) ** 2
)
)
1.5681439279637486
@qfunc
def main(
phase_reg: Output[QNum[NUM_PHASE_QUBITS, UNSIGNED, NUM_PHASE_QUBITS]],
) -> None:
state_reg = OracleVars()
allocate(state_reg)
allocate(phase_reg)
sp_oracle(state_reg)
qpe(
unitary=lambda: my_grover_operator(
arith_oracle,
sp_oracle,
state_reg,
),
phase=phase_reg,
)
Synthesizing the Model to a Quantum Program
constraints = Constraints(max_width=14)
qmod_qpe = create_model(
main,
constraints=constraints,
preferences=Preferences(optimization_level=1),
out_file="quantum_counting_qpe",
)
qprog_qpe = synthesize(qmod_qpe)
show(qprog_qpe)
Quantum program link: https://platform.classiq.io/circuit/2yh9VkXrQKRSzdGz1dVc9JtNIgn
Executing the Quantum Program
result = execute(qprog_qpe).result_value()
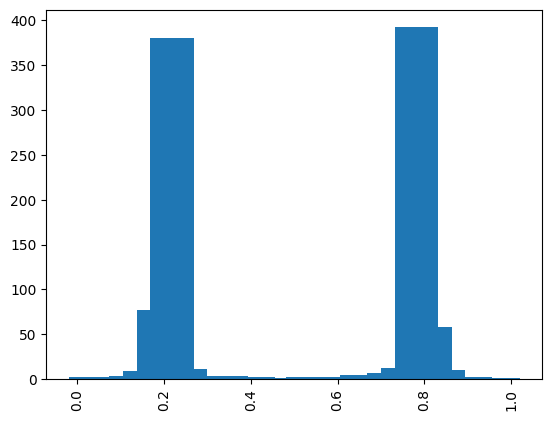
Upon plotting the resulting histogram, we see two phase values with high probability (however, both correspond to the same amplitude). Note that phase_reg is already coded as fixed QNum in the range [0,1].
import matplotlib.pyplot as plt
phases_counts = dict(
(sampled_state.state["phase_reg"], sampled_state.shots)
for sampled_state in result.parsed_counts
)
plt.bar(phases_counts.keys(), phases_counts.values(), width=0.1)
plt.xticks(rotation=90)
print("phase with max probability: ", max(phases_counts, key=phases_counts.get))
phase with max probability: 0.21875
From the phase, we can extract the number of solutions:
expected_num_solutions = 6
solutions_ratio_qpe = np.sin(np.pi * max(phases_counts, key=phases_counts.get)) ** 2
print(
"Number of solutions: ",
(2**DOMAIN_SIZE) * solutions_ratio_qpe,
)
assert np.isclose(
(2**DOMAIN_SIZE) * solutions_ratio_qpe, expected_num_solutions, atol=1.5
)
Number of solutions: 6.439277423870974
Amplitude Estimation Using Iterative Quantum Amplitude Estimation
Now we are ready for the iterative method.
Instead of QPE, the algorithm applies the unitary
where \(m\), the number of repetitions, changes between iterations of the algorithm.
There is one subtlety that changes the way we work with the Grover operator. The classical algorithm expects an additional indicator qubit that marks the "good" states, i.e.:
So now, most of our logic goes into the state preparation oracle (\(A\)). It combines the loading of the solution space with setting the indicator qubit.
@qfunc
def iqae_state_preparation(vars: OracleVars, ind: QBit):
hadamard_transform(vars)
arith_equation(vars, ind)
Wrapping All to the Iterative Quantum Amplitude Estimation Algorithm
We use the built-in IQAE class that the quantum code for the algorithm as well as the classical execution code. The circuit starts with the state \(A|0\rangle\), then applies iterations of the Grover operator.
Note that the algorithm applies a varied number of Grover iterations on each execution. The number of iterations is chosen dynamically based on previous execution results, using statistical inference methods. It expects a state preparation function that creates the following state:
Where the indicator qubit is marking the wanted state.
from classiq.applications.iqae.iqae import IQAE
iqae = IQAE(
state_prep_op=iqae_state_preparation,
problem_vars_size=DOMAIN_SIZE,
constraints=Constraints(optimization_parameter="width"),
preferences=Preferences(optimization_level=1),
)
Synthesizing the Model to a Quantum Program
qmod = iqae.get_model()
write_qmod(qmod, "quantum_counting_iqae", decimal_precision=10)
qprog_iqae = iqae.get_qprog()
show(qprog_iqae)
Quantum program link: https://platform.classiq.io/circuit/2yhAKFEUmFv32ggbGstcSqWwOJL
Executing the Quantum Program
iqae_result = iqae.run(
epsilon=1 / (2**DOMAIN_SIZE * 2),
alpha=0.01, # desired error # desired probability for error
)
We set \(\epsilon = 1/{2^4} \cdot 0.5 = 1/32\). alpha is the tail probability of estimating the result with accuracy \(\epsilon\).
print(
f"Number of solutions: {(2**DOMAIN_SIZE) * iqae_result.estimation}, accuracy: "
f"{(2**DOMAIN_SIZE)*(iqae_result.confidence_interval[1]-iqae_result.confidence_interval[0])}"
)
Number of solutions: 6.005168918888571, accuracy: 0.09728649576021553
assert np.isclose(
(2**DOMAIN_SIZE) * iqae_result.estimation, 6, atol=1 / (2**DOMAIN_SIZE - 1)
)
We can also see the statistics of the IQAE execution:
for i, iteration in enumerate(iqae_result.iterations_data):
print(
f"iteration_id: {i}, num grover iterations: {iteration.grover_iterations}, counts: {iteration.sample_results.counts}"
)
iteration_id: 0, num grover iterations: 0, counts: {'1': 758, '0': 1290}
iteration_id: 1, num grover iterations: 6, counts: {'1': 1161, '0': 887}
References
[1]: Quantum Counting Algorithm, Wikipedia.
[2]: Grinko, D., Gacon, J., Zoufal, C. et al. Iterative quantum amplitude estimation. npj Quantum Inf 7, 52 (2021).
[3]: Brassard, G., Hoyer, P., Mosca, M., & Tapp, A. (2002). Quantum Amplitude Amplification and Estimation. Contemporary Mathematics, 305, 53-74.