Skip to content

Design - Quantum Operations

View on GitHub Experiment in the IDE

Quantum computing resembles classical computing in some aspects, and is substantially different in other aspects. One of the key advantages of Qmod is that it captures uniquely quantum core concepts in a simple and natural way. This begins with the quantum objects and variables described in the previous tutorial (see Quantum Variables and Functions) and continues with the meaningful native quantum operations.

Simply put, quantum operations are functions of functions applied on quantum objects that are very common in quantum computing, hence receiving a special place in the Qmod language. More accurately, these are built-in statements in the Qmod language. A statement is a building block of a programming language, such that programming languages are composed from statements. For example, if and for loops are common statements in programming languages such as Python.

There are a few quantum operation statements in Qmod, and here we focus on arguably the most useful one: control. It applies a specified quantum function conditioned on some state (value) of a given quantum variable. Other quantum operations are invert, power, and within_apply. See all the quantum operations here.

Examine the control statement using a concrete example.

Concrete Example

The task is to prepare a quantum number x in a superposition of all possible integers between \(0\) to \(15\), i.e., \(|x\rangle = \frac{1}{\sqrt{16}}(|0\rangle + |1\rangle + \dots + |15\rangle)\). Then, prepare another quantum number y that is in the state \(|17\rangle\) only if \(|x\rangle\) is in the state \(|15\rangle\), otherwise the state of y should be \(|0\rangle\). Mathematically, the task is to prepare this state: \(\begin{equation} |x\rangle|y\rangle = \frac{1}{\sqrt{16}}(|0\rangle|0\rangle+|1\rangle|0\rangle+\dots+|14\rangle|0\rangle+|15\rangle|17\rangle). \end{equation}\)

How to approach this task? You have already seen how to create a uniform superposition with the hadamard_transform. Now, conditioned on the value of \(|x\rangle\) being \(|15\rangle\), prepare the state of \(|y\rangle\) to be \(|17\rangle\) with the inplace_xor function.

Numeric Assignment Numeric assignments provide simple operations (using Qmod and SDK) and functions (SDK only) for performing arithmetic and logical operations. The `inplace_xor` is the fufunction is equivalent to the `^=` operation. In the SDK, lambda (as a function rather than an operation). Read more [here](https://docs.classiq.io/latest/qmod-reference/language-reference/statements/numeric-assignment/). 
from classiq import *


@qfunc
def apply_control(x: QNum, y: QNum):
    control(ctrl=(x == 15), stmt_block=(lambda: inplace_xor(17, y)))

In the Python syntax, control is a Python function with two arguments. The ctrl argument is the condition for which the stmt_block operand is applied. The stmt_block argument is the specific operation/function to apply, given that the condition is satisfied. Passing a function as an argument for another function is done with the lambda: keyword. So, anytime you pass a function as an argument in the Python SDK, use the prefix lambda:.

More on `lambda:` The `lambda:` keyword is used to define inline functions.

In the native syntax, control is embedded in the Qmod language such that the condition is specified with the () parentheses, and the operand to apply is specified within the scope of the control, i.e., within the {} curly brackets.

Now for the main function. In the end, you want to evaluate the execution results of both x and y so both of them are arguments of the main function. Initialize x with \(4\) qubits because it needs to be in a superposition of \(16 (=2^4)\) states, and initialize y with \(5\) qubits because this is the minimum number of qubits required to represent the number \(17\) (\(ceiling(log_2(17))=5\)).

@qfunc
def main(x: Output[QNum], y: Output[QNum]):
    allocate(4, x)
    allocate(5, y)

    hadamard_transform(x)
    apply_control(x, y)

Prepare the initial superposition by applying hadamard_transform on x and the apply_control function you defined earlier on both x and y.

That's it! You can now synthesize and view the quantum program:

quantum_program = synthesize(create_model(main))
show(quantum_program)

To receive the execution results, execute the quantum program:

job = execute(quantum_program)
results = job.result()[0].value.parsed_counts
print(results)

[{'x': 1, 'y': 0}: 150, {'x': 0, 'y': 0}: 141, {'x': 4, 'y': 0}: 140, {'x': 3, 'y': 0}: 140, {'x': 8, 'y': 0}: 133, {'x': 15, 'y': 17}: 132, {'x': 10, 'y': 0}: 132, {'x': 14, 'y': 0}: 131, {'x': 9, 'y': 0}: 131, {'x': 13, 'y': 0}: 123, {'x': 11, 'y': 0}: 120, {'x': 12, 'y': 0}: 120, {'x': 2, 'y': 0}: 118, {'x': 6, 'y': 0}: 117, {'x': 5, 'y': 0}: 115, {'x': 7, 'y': 0}: 105]

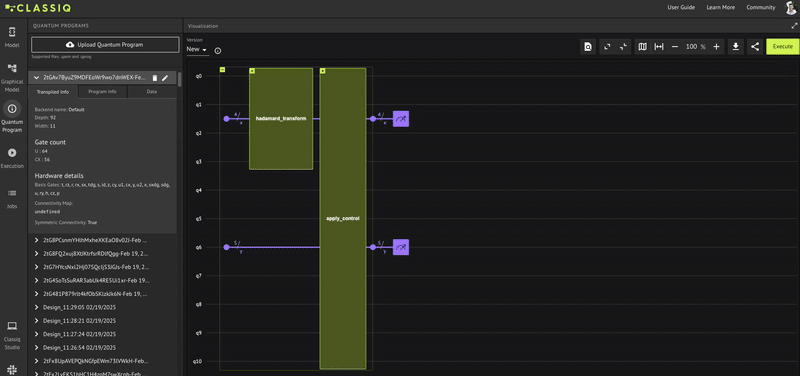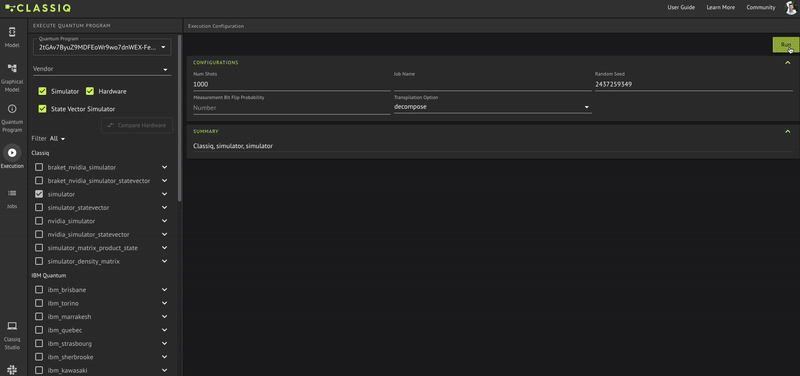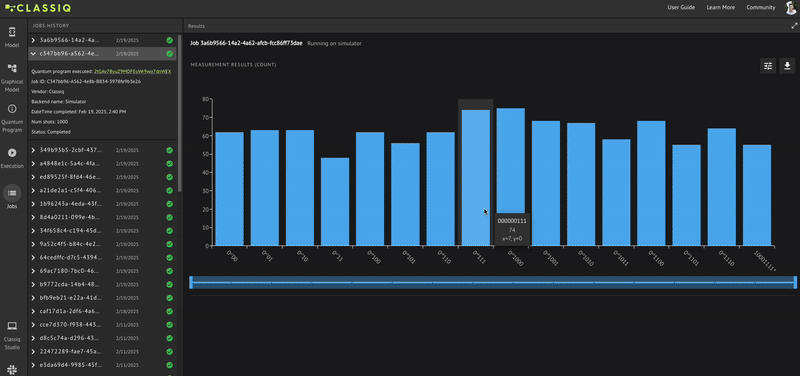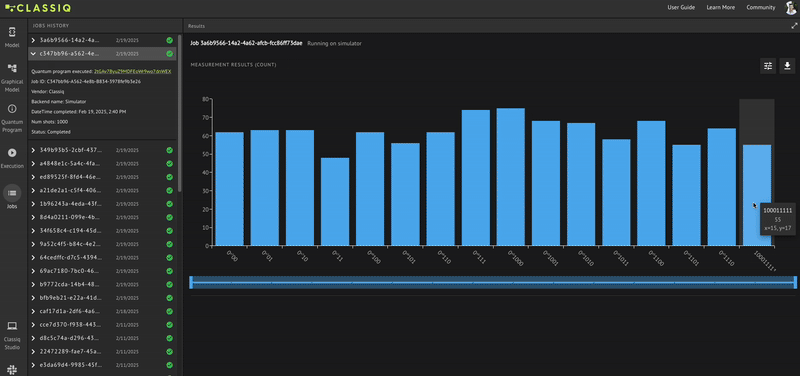
See that you receive \(16\) possible values for x and y, and \(y=0\) in all the pairs of values except when \(x=15\), as defined!

Summary - Quantum Operations

These are the main takeaways from the example in terms of quantum operations:

  • Quantum operations receive both quantum objects and quantum functions as inputs, and they apply the quantum functions on the quantum objects according to the nature of the quantum operation. In the above example, the control operation applies the inplace_xor function on the quantum variable y conditioned on the value of the quantum variable x being \(15\).

  • In the native syntax, the quantum operations are statements of the Qmod language and have a special syntax. In the above example, the syntax for control is control(){;} where the condition is given in parentheses and the applied operation/function is in curly brackets.

  • In the Python SDK, write the quantum operations just like any other Python function. The arguments of the quantum operation that are functions by themselves must be passed with the lambda: keyword. In the above example, the stmt_block argument of the control function is a function by itself (inplace_xor), hence it is prefixed with lambda:.

  • Other quantum operations are power (raising a unitary to some power), invert (applying the inverse of a unitary), and within_apply (applying two unitaries \(U\) and \(V\) as \(UVU^\dagger\)). See a detailed description of the quantum operators.

write_qmod(create_model(main), "quantum_operations")