Discrete Quantum Walks
"Quantum Walk" is an approach for developing and designing quantum algorithms. It can be thought as a quantum analogy to classical random walk. This generic technique underlies many quantum algorithms, in particular, the Grover's search algorithm, can be viewed as a quantum walk.
In similar to classical random walks, quantum walks are divided into the discrete case and the continuos one. This notebook focuses on discrete quantum walks, and is organized as follows: First, we give a one to one comparison between classical random walks and quantum walks, by treating a specific example: a walk on a circle. Then, we define a general quantum model for studying quantum walks, and consequently apply it to the circle case and to a a hypercube graph.
This tutorial demonstrates the following concepts of Classiq:
* The resemblance between classical and quantum programming with Classiq.
* Classiq's built-in constructs:
* control: general controlled-logic
* power: "parametric power", specified as execution parameter.
* numeric quantum types: working with signed and unsigned integers.
* within_apply : for compute/uncompute operations \(U V U^{\dagger}\).
* Passing a list of QCallables (quantum functions).
* Parsed execution results, according to quantum variable types.
Classical Random Walks vs. Quantum Walks
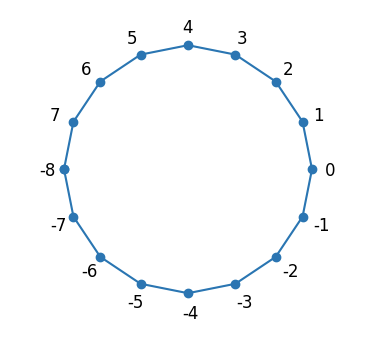
We first specify and implement a simple example: a discrete walk on a circle, or more precisely, on a regular polygon having \(2^N\) nodes (see Figure 1 below). The idea of random/quantum walk is the following: 1. We start at some initial point, e.g., the zeroth node. 2. We flip a coin, if we get heads/tails we move one step clockwise/counter-clockwise. 3. We repeat steps 1-2 for a given total number of steps \(T\).
import matplotlib.pyplot as plt
import numpy as np
from classiq import *
Let us code a classical random walk and a discrete quantum walk side by side:
First, we define a function to flip a coin: * Classical: the coin is either 0 or 1, to flip a coin we simply draw a random number from the set \(\{0,1\}\). * Quantum: the coin is represented by a qubit, a "flip" is defined by some unitary operation on it. We choose the Hadamard gate, which sends the \(|0\rangle\) state into an equal superposition of \(|0\rangle\) and \(|1\rangle\).
def classical_coin_flip(coin):
return np.random.randint(2)
@qfunc
def quantum_coin_flip(coin: QBit):
H(coin)
Next, we define a function for moving clockwise and counterclockwise. This operation is simply a modular addition by \(\pm 1\). * Classical: the position is an integer in \([-2^{N-1}, 2^{N-1}-1]\), we use basic arithmetic operations. * Quantum: the position is an \(N\)-qubits state. We can easily build an inplace modular addition by 1 ourselves (see explanation at the end of this notebook). Note that since quantum operations are reversible, we can define a counterclockwise step as the inverse of the clockwise step.
from classiq.qmod.symbolic import pi
# classical
def classical_step_clockwise(x, circle_size):
return (x + 1) % circle_size
def classical_step_counterclockwise(x, circle_size):
return (x - 1) % circle_size
# quantum
@qfunc
def quantum_step_clockwise(x: QArray):
within_apply(
lambda: qft(x),
lambda: repeat(x.len, lambda i: PHASE(2 * pi * 2 ** (i) / (2**x.len), x[i])),
)
Finally, we construct a function for the full walk, iterating over flipping a coin and a single walking step based on the coin's state. Note the difference between the classical and quantum functions' declarations, for the quantum part we do not need to pass the circle size, as it is given by the size of the position state \(x\).
# classical
def random_walk_circle(
time, # total time
x, # position
circle_size, # the size of the circle
):
coin = 0
for step in range(time):
coin = classical_coin_flip(coin)
if coin == 0:
x = classical_step_clockwise(x, CIRCLE_SIZE)
if coin == 1:
x = classical_step_counterclockwise(x, CIRCLE_SIZE)
return x
# quantum
@qfunc
def discrete_quantum_walk_circle(
time: CInt, # total time
x: QArray[QBit], # position
):
coin = QNum("coin")
allocate(1, coin)
power(
time,
lambda: (
quantum_coin_flip(coin),
control(coin == 0, lambda: quantum_step_clockwise(x)),
control(coin == 1, lambda: invert(lambda: quantum_step_clockwise(x))),
),
)
Let us define and run a specific example. We take a circle of size \(2^7\), a total time of 50 steps, and 10000 samples.
CIRCLE_SIZE = 2**7
TOTAL_TIME = 50
NUM_SAMPLES = 10000
from classiq.execution import ExecutionPreferences
from classiq.qmod.symbolic import floor, log
# classical
final_pos = np.zeros(CIRCLE_SIZE)
for sample in range(NUM_SAMPLES):
x = random_walk_circle(time=TOTAL_TIME, x=0, circle_size=CIRCLE_SIZE)
final_pos[x] += 1
# quantum
@qfunc
def main(t: CInt, x: Output[QNum]):
allocate_num(floor(log(CIRCLE_SIZE, 2)), True, 0, x)
discrete_quantum_walk_circle(t, x)
@cfunc
def cmain():
save({"run": sample({"t": 50})})
qmod = create_model(
main,
classical_execution_function=cmain,
execution_preferences=ExecutionPreferences(num_shots=NUM_SAMPLES),
)
write_qmod(qmod, "quantum_walk_circle")
qprog = synthesize(qmod)
show(qprog)
results = execute(qprog).result()
Opening: https://platform.classiq.io/circuit/cfd073b1-0ec3-4490-b8ee-0837975e4ea0?version=0.41.0.dev39%2B79c8fd0855
We can plot the probabilities of ending at each position along the circle. In both cases, classical and quantum, we consider the probability of the final position after time \(T=50\).
# classical
prob_classical = final_pos / NUM_SAMPLES
grid = (np.linspace(0, CIRCLE_SIZE - 1, CIRCLE_SIZE)).astype(int)
flipped_grid = np.append(
grid[CIRCLE_SIZE // 2 : CIRCLE_SIZE] - CIRCLE_SIZE, grid[0 : CIRCLE_SIZE // 2]
)
flipped_prob_classical = np.append(
prob_classical[CIRCLE_SIZE // 2 : CIRCLE_SIZE], prob_classical[0 : CIRCLE_SIZE // 2]
)
# quantum
quantum_probs = {
sample.state["x"]: sample.shots / NUM_SAMPLES
for sample in results[0].value.parsed_counts
}
sorted_quantum_probs = dict(sorted(quantum_probs.items()))
plt.plot(flipped_grid, flipped_prob_classical, ".-")
plt.plot(sorted_quantum_probs.keys(), sorted_quantum_probs.values(), ".-")
plt.xlabel("position", fontsize=16)
plt.ylabel("probability", fontsize=16)
Text(0, 0.5, 'probability')
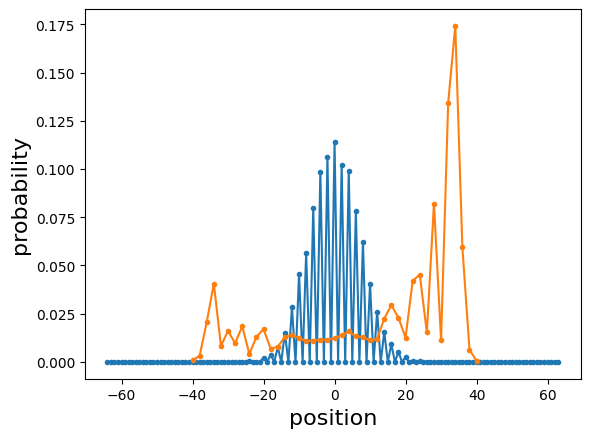
We can see a clear difference between the two distributions. The classical distribution is symmetric around the zero position, whereas the quantum example is asymmetric with a peak far from 0. This is a small example of the different behaviors of classical random walks and quantum walks. More details and examples can be found in Ref. [1].
How to Build a General Quantum Walk with Classiq
We define a quantum function for a discrete quantum walk. The arguments of the function are:
* time: an integer for the number of walking steps.
* coin_flip_qfunc: the quantum function for "flipping" the coin.
* walks_qfuncs: a list of quantum functions for all possible transitions at a given point.
* coin_state: the quantum state of the coin.
from classiq.qmod.symbolic import pi
@qfunc
def discrete_quantum_walk(
time: CInt,
coin_flip_qfunc: QCallable[QNum],
walks_qfuncs: QCallableList,
coin_state: QNum,
):
power(
time,
lambda: (
coin_flip_qfunc(coin_state),
repeat(
walks_qfuncs.len,
lambda i: control(coin_state == i, lambda: walks_qfuncs[i]()),
),
),
)
Example: Symmetric Quantum Walk on a Circle
As a first example, we can consider the circle geometry from above, implemented with our generic definition. However, as opposed to the implementation above we take a different initial condition for the coin, \(\frac{1}{\sqrt{2}}(|0\rangle +i |1\rangle)\) instead of \(|0\rangle\). This state is a balanced initial condition for the coin (see Ref. [1]) and can be prepared by applying an H gate followed by an S gate.
from classiq.execution import ExecutionPreferences
CIRCLE_SIZE = 2**7
NUM_SHOTS = 1e4
@qfunc
def main(t: CInt, x: Output[QNum]):
coin = QBit("coin")
allocate_num(floor(log(CIRCLE_SIZE, 2)), True, 0, x)
allocate(1, coin)
H(coin)
S(coin)
discrete_quantum_walk(
t,
lambda coin: H(coin),
[
lambda: quantum_step_clockwise(x),
lambda: invert(lambda: quantum_step_clockwise(x)),
],
coin,
)
@cfunc
def cmain():
save({"run1": sample({"t": 50})})
qmod = create_model(
main,
classical_execution_function=cmain,
execution_preferences=ExecutionPreferences(num_shots=NUM_SHOTS),
)
Now that our model is defined we can synthesize, execute and plot the outcome probability:
qprog = synthesize(qmod)
write_qmod(qmod, "quantum_walk_circle_balanced_coin")
show(qprog)
results = execute(qprog).result()
quantum_probs = {
sample.state["x"]: sample.shots / NUM_SAMPLES
for sample in results[0].value.parsed_counts
}
sorted_quantum_probs = dict(sorted(quantum_probs.items()))
plt.plot(sorted_quantum_probs.keys(), sorted_quantum_probs.values(), ".-")
plt.xlabel("position", fontsize=16)
plt.ylabel("probability", fontsize=16)
Opening: https://platform.classiq.io/circuit/a430e208-f365-47e7-a7fc-0b0b99fc4743?version=0.41.0.dev39%2B79c8fd0855
Text(0, 0.5, 'probability')
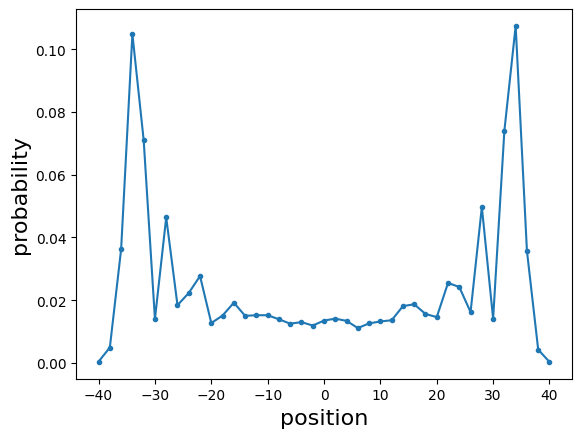
We can see that now the distribution is symmetric. Clearly, the distribution of a quantum walk on a circle depends on the initial condition for the coin. This is another example of the peculiar behavior of quantum walks, with respect to classical random walks.
Example: 4D Hypercube with a Grover Coin
Next, we consider an hypercube graph (see Figure 3). The quantum walk on a hypercube shows a completely different behavior compared to classical counterpart. One striking difference refers to the hitting time: the time it takes to reach node \(v\) starting from an initial node \(u\). In particular, an interesting question is the hitting time between one corner of the hypercube "000..0" to the opposite one "111...1". In Ref. [2]) it was shown that the hitting time for the hypercube in quantum walks is exponentially faster than the analog quantity in classical random walks. The rigour definition of the "hitting time" in the quantum case is nontrivial, and different definitions are relevant. In this notebook we do not use the exact definition, but simply demonstrate a specific result, highlighting the result of Ref. [2].
We define \(P_{\rm corner}(T)\) as the probability of measuring the walker at the opposite corner \(|2^{N}-1\rangle\) after \(T\) steps, starting at position \(|0\rangle\) at time 0. We examine this quantity for the quantum and the classical case.
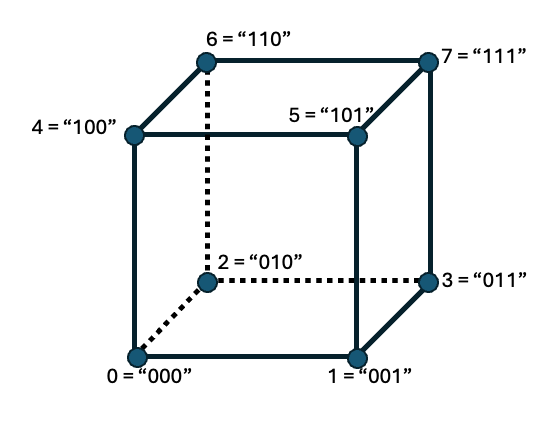
First, we define a model for quantum walk on a hypercube. Two nodes in the hypercube are connected to each other iff their Hamming distance is 1. Thus, a step along a hypercube is given by moving "1 Hamming distance away". For a \(d\)-dimentional hypercube, at each node there are \(d\) possible directions to move, each of them is given by applying a bit flip on one of the bits. In the quantum case, this is obtained by applying an X gate on on of the \(N\) qubit.
Concerning the coin operator we take the so-called "Grover diffuser" function. This choice refers to a symmetric quantum walk [1]. The Grover diffuser operator is a reflection around a given state \(|\psi\rangle\):
where I is the identity matrix. In the \(N\)-dimensional hypercube each node is connected to \(N\) nodes, thus, the coin state should include \(N\) different states. Therefore, the coin is represented by a quantum variable of size \(\lceil \log_2(N)\rceil\), and the Grover diffuser is defined with:
We now build our model, using the grover_diffuser function from Classiq's open library.
@qfunc
def moving_one_hamming_dist(pos: CInt, x: QArray[QBit]):
X(x[pos])
from classiq.execution import ExecutionPreferences
from classiq.qmod.symbolic import ceiling
SPACE_SIZE = 4
NUM_SHOTS = 1e4
# in the case the space size is not 2^r we padd the coin state with zeros
reduced_coin_state = [1 / SPACE_SIZE] * SPACE_SIZE + [0] * int(
2 ** np.ceil(np.log2(SPACE_SIZE)) - SPACE_SIZE
)
@qfunc
def main(
t: CInt,
x: Output[QArray[QBit]],
):
# start at zero state location
allocate(SPACE_SIZE, x)
# start with equal superpositon for the relevant states.
coin = QArray("coin")
prepare_state(reduced_coin_state, 0.0, coin)
discrete_quantum_walk(
t,
lambda coin: grover_diffuser(
lambda coin: inplace_prepare_state(reduced_coin_state, 0.0, coin), coin
),
[
lambda: moving_one_hamming_dist(0, x),
lambda: moving_one_hamming_dist(1, x),
lambda: moving_one_hamming_dist(2, x),
lambda: moving_one_hamming_dist(3, x),
],
coin,
)
@cfunc
def cmain():
save({"run": sample({"t": 4})})
qmod = create_model(
main,
classical_execution_function=cmain,
execution_preferences=ExecutionPreferences(num_shots=NUM_SHOTS),
constraints=Constraints(optimization_parameter="width"),
)
write_qmod(qmod, "quantum_walk_hypercube")
qprog = synthesize(qmod)
show(qprog)
Opening: https://platform.classiq.io/circuit/c674bb1e-ca9f-4d56-b2a1-e74797d25ec2?version=0.41.0.dev39%2B79c8fd0855
results = execute(qprog).result()
print(
"The probability to reach the opposite corner:",
results[0].value.counts.get("1" * SPACE_SIZE, 0) / NUM_SHOTS,
)
The probability to reach the opposite corner: 0.56
We found that at \(T=4\) the probability to measure the walker at the opposite corner is larger than \(1/2\). We can check an analogous question in the classical random walk, where the distribution is taken over an ensemble of independent experiments):
initial_point = 0
final_point = dict()
for sample in range(NUM_SAMPLES):
coin_state = np.random.randint(SPACE_SIZE)
for k in range(SPACE_SIZE):
if coin_state == k:
temp_point = initial_point ^ 2**k
initial_point = temp_point
final_point[initial_point] = final_point.get(initial_point, 0) + 1
print(
"The probability to reach the opposite corner in the classical case:",
final_point.get(2**SPACE_SIZE - 1, 0) / NUM_SAMPLES,
)
The probability to reach the opposite corner in the classical case: 0.0658
For the classical analogous case, the probability is much lower. This is a manifestation of the fact that the hitting time in a hypercube is exponentially shorter in quantum walks, in comparison to classical random walks.
Technical Notes
QFT modular adder
Below we explain the quantum_step_clockwise function defined for the quantum walk on a circle. The unitary matrix that represents walking on a circle operates as follows:
$$
U_{+}|i\rangle =
\left{
\begin{array}{l l}
|i+1\rangle & {\text{if } } i\neq 2^{N-1}\
|0\rangle & {\text{if } } i = 2^{N-1}
\end{array}
\right.
U_+ = \begin{pmatrix} 0 & 1 & 0 & \cdots & 0 & 0 \ 0 & 0 & 1 & 0 & \cdots & 0 \ 0 & \ddots &\ddots & \ddots & \cdots & 0 \ \vdots & \ddots & \ddots & \ddots& \ddots & \vdots \ 0 & \ddots & \ddots & 0& 0 & 1\ 1 & 0 & 0 & \cdots & 0 & 0 \end{pmatrix}.
U_+ = \mathcal{FT} \cdot \begin{pmatrix} \alpha^0 & 0 & \cdots& \cdots & 0 \ 0 & \alpha^1 & 0 & \cdots & 0 \ 0 & 0 &\ddots & \cdots & 0 \ 0 & 0 &\cdots & \alpha^{2^N-2} & 0 \ 0 & \cdots & 0 & \cdots & \alpha^{2^N-1} \end{pmatrix} \cdot \mathcal{FT}^{\dagger}, $$ with \(\alpha=e^{2\pi i /2^N }\). We can implement both the \(\mathcal{FT}\) matrix and the diagonal matrix efficiently on a quantum computer, the former by a QFT and the latter by applying a series of \(N\) RZ rotations.
[1]: Kempe, J. "Quantum random walks: an introductory overview." Contemporary Physics 44, 307 (2003).
[2]: Kempe, J. "Discrete quantum walks hit exponentially faster." Probability theory and related fields 133, 215 (2005).