Hadamard Test

View on GitHub Experiment in the IDE

The Hadamard test [1] is a widely-used [2,3] quantum primitive that provides an elegant method to compute the real part of an expectation value of a given unitary for some target state. Many problems require evaluating the expectation value of a unitary operator for a prepared state, and the Hadamard test offers an intuitive alternative to the traditional methods of decomposing the unitary into Pauli strings and measuring each non-commutative string independently.

The Hadamard test is a special case of the linear combination of unitaries (LCU) primitive, which is covered in a separate section. The SWAP test, another special case of the LCU, may be viewed as a variation of the Hadamard test.

The overall implementation consists of three functional building blocks followed by a measurement step, as illustrated in the scheme below:

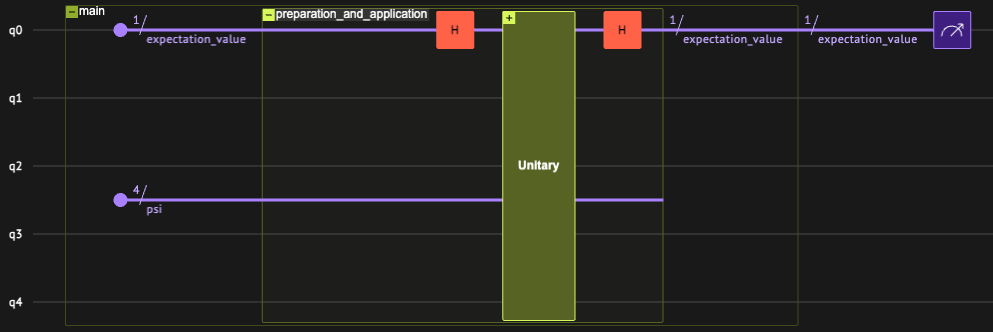
To implement the Hadamard test algorithm with a unitary $U$ and target state $|{\psi}\rangle$ as inputs and control-qubit probabilities as the outputs, a Hadamard gate $H$ is first applied to place the control qubit in a uniform superposition $\frac{1}{\sqrt{2}}\big(|{0}\rangle|{\psi}\rangle+|{1}\rangle|{\psi}\rangle\big)$. Next, a controlled unitary gate is applied to the target qubit array, resulting in the state $\frac{1}{\sqrt{2}}\big(|{0}\rangle|{\psi}\rangle+|{1}\rangle U|{\psi}\rangle\big)$. Another Hadamard gate $H$ is then applied to the control qubit, yielding $\frac{1}{2}\big(|{0}\rangle\big(\mathbb{I}+U\big)|{\psi}\rangle+|{1}\rangle\big(\mathbb{I}-U\big)|{\psi}\rangle\big)$, after which a final measurement is performed on the control qubit. The probability of measuring the control qubit in state $|{0}\rangle$, given by $P(0)=||\frac{1}{2}\big(\mathbb{I}+U\big)|{\psi}\rangle||^2$, enables the calculation the real part of the expectation value $\langle\psi|U|\psi\rangle$ in a post-processing step, through the simple algebraic operation $\text{Re}\langle\psi|U|\psi\rangle=2P(0)-1$. A different algebraic operation can be used to retrieve the imaginary part of the expectation value.

You can refer to the Mathemtaical Description section describing the full mathematical derivation of a general Hadamard test implementation.

In this tutorial, we will implement a Hadamard test for the Quantum Fourier Transform (QFT) unitary $U_{QFT}$ (read more), acting on a 4-qubit target state $|0000\rangle$ using the Classiq IDE/ SDK. This implementation leverages Classiq's high-level functional design utilities, following the functional block structure outlined above.

NOTE: Quantum Fourier Transform

The Quantum Fourier Transform (QFT) function is the quantum analog for the discrete Fourier transform. It is applied on the quantum register state vector in the following manner:

\[U_{QFT}|{j}\rangle=\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}e^{\frac{2\pi i}{2^n}jk}|{k}\rangle=\otimes_{t=1}^n\frac{1}{\sqrt{2}}\big(|{0}\rangle+e^{\frac{2\pi i}{2^{t}}j}|{1}\rangle)\]

Where $j$ and $k$ are the binary numbers the $n$ qubits represent. more information

Guided Implementation

To implement the Hadamard test for the QFT unitary $U_{QFT}$ and the state $|0000\rangle$, one control qubit and an array of four target qubits are initialized. The control qubit variable will be named expectation_value and is of QBit type, and the target qubit array will be captured by the QArray type variable psi. All qubits are initialized in $|0\rangle$ states, and the state of the psi qubit array will remain unchanged throughout the implementation ($|0000\rangle$).

Our implementation of the Hadamard test involves three main steps, followed by a measurement of the expectation_value qubit and a post-processing step to obtain the real part of the expectation value:

1) Applying the Hadamard gate $H$ to the expectation_value qubit as a preparation step, creating a uniform superposition.

2) Applying the unitary gate $U_{QFT}$ on the psi qubit array in a controlled manner, conditioned on the control qubit being in the $|{1}\rangle$ state.

3) Re-application of a Hadamard gate $H$ to the control qubit that can be seen as an inverse preparation step, with $H$ acting as its own inverse.

4) A projective measurement of the expectation_value qubit, yielding the probabilities of measuring it in the $|0\rangle$ and $|1\rangle$ states. The probability $P(0)$ of being in the $|0\rangle$ state is then algebraically manipulated in a post-processing step to yield the real part of the expectation value by using the expression $2P(0)-1$.

We begin by defining the function controlled_qft that implements the controlled operation of the unitary $U_{QFT}$ on psi, conditioned on the control qubit expectation_value is in the $|{1}\rangle$ state. This is achieved by leveraging the Classiq built-in control and qft functions:

from classiq import *


@qfunc
def controlled_qft(expectation_value: QBit, psi: QArray):
    control(expectation_value, lambda: qft(psi))

Next, We define the function preparation_and_application, seamlessly implementing the three main steps of the Hadamard test as outlined above, using the Classiq Within-Apply statement (read more). The Within-Apply statement performs the operation $V^{\dagger}UV$, specifically designed for situations where a preparation step is performed solely to enable the operation of a particular function and is subsequently inverted. The preparation and inverse-preparation actions should be specified within the Within section, while the primary function operating should be specified in the Apply section.

Since the third step, which involves the re-application of the Hadamard gate to the expectation_value qubit can be regarded as an inverse-preparation step (due to $H$ being its own inverse), the Hadamard test becomes a natural candidate for the Within-Apply statement.

The preparation stage, which involves applying a Hadamard gate $H$ to the expectation_value qubit, and the re-application of the Hadamard gate to the same qubit after the controlled QFT operation on the psi qubit array are both managed within the Within section. The function controlled_qft, which handles the controlled operation of $U_{QFT}$ on the psi qubit array, is specified in the Apply section:

@qfunc
def preparation_and_application(expectation_value: QBit, psi: QArray):
    within_apply(
        within=lambda: H(expectation_value),
        apply=lambda: controlled_qft(expectation_value, psi),
    )

Finally, we define a main function that encapsulates all essential components of the algorithm. It begins with the declaration and initialization of all qubits, followed by a call to the preparation_and_application function, which implements the three core steps:

@qfunc
def main(expectation_value: Output[QBit]):
    psi = QArray("psi")
    allocate(out=expectation_value, num_qubits=1)
    allocate(out=psi, num_qubits=4)
    preparation_and_application(expectation_value, psi)


qmod = create_model(main)
qprog = synthesize(qmod)
show(qprog)

Opening: https://platform.classiq.io/circuit/f8f96fff-7a3f-4bf5-9217-db3964cf3b6e?version=0.60.0

While the code is elegantly structured, the resulting quantum program could be highly complex. The Classiq synthesis engine expertly manages this complexity, transforming the high-level code into a fully optimized quantum circuit according to your optimization preferences.

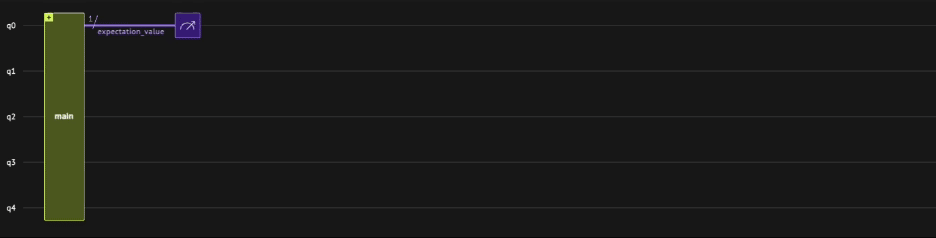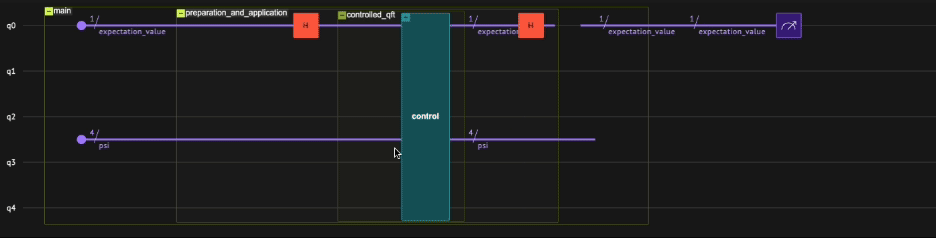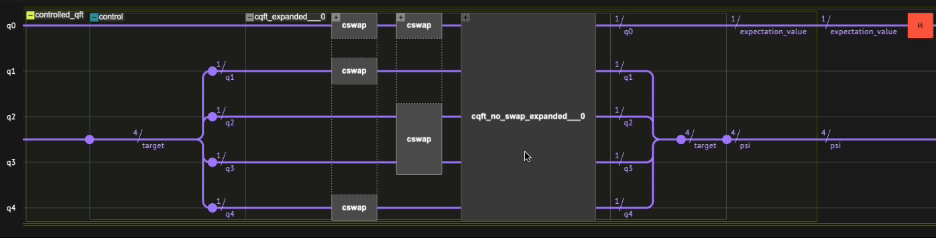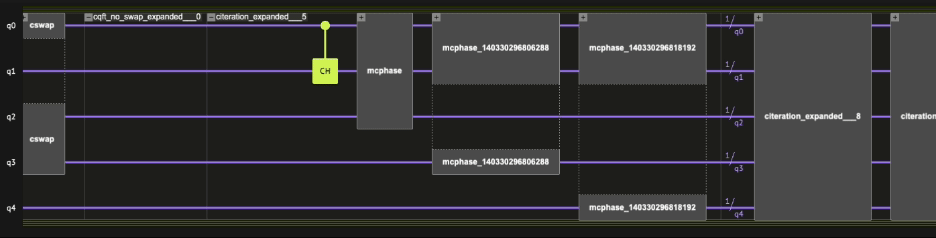
gif showing the expansion of the different building blocks

By declaring psi as a local variable in the main function (in contrast to expectation_value, which is declared globally), the execution of the quantum program on the Classiq simulator will yield the measurement outcomes of the expectation_value qubit in states $|{0}\rangle$ and $|{1}\rangle$, along with the corresponding measurement probabilities. The probability $P(0)$ can then be algebraically manipulated to calculate the real part of the expectation value, which should align with the analytical result:

\[\text{Re}\big(\langle 0000|U_{qft}|0000\rangle\big)=\langle 0000|++++\rangle= 0.25\]

You can refer to the note below for the complete derivation.

Complete derivation

After the execution of the main function, the system is evolved into its final quantum state:

\[\frac{1}{2}\Big(|{0}\rangle\big(\mathbb{I}+U_{QFT}\big)|{0000}\rangle+|{1}\rangle\big(\mathbb{I}-U_{QFT}\big)|{0000}\rangle\Big)=\frac{1}{2}\Big(|{0}\rangle\big(|{0000}\rangle+|{++++}\rangle\big)+|{1}\rangle\big(|{0000}\rangle-|{++++}\rangle\big)\Big)\]

Since applying QFT on $|{0000}\rangle$ is equivalent to applying a 4-qubit Hadamard transform, transforming it to the $|{++++}\rangle$ state.

Running the program on the Classiq simulator outputs the measurement results for both states of the control qubits, which can be analytically calculated and compared:

\[P(0)=\frac{1}{4}|||{0000}\rangle+|{++++}\rangle||^2=\frac{1}{2}\big(1+\frac{1}{4}\big)=0.625,\;\;\;\;\;\;\;\; P(1)=\frac{1}{4}|||{0000}\rangle-|{++++}\rangle||^2=\frac{1}{2}\big(1-\frac{1}{4}\big)=0.375\]

where the result of the inner product $\langle 0000|++++\rangle=\frac{1}{4}\langle 0000|0000\rangle=\frac{1}{4}$ is used.

The probabilities can then be manipulated to calculate the expectation value as $\text{Re}\big(\langle 0000|U_{qft}|0000\rangle\big)=2P(0)-1=0.25$, yielding the same result as the direct calculation provided above in the main text.

Now, let us verify this by executing the quantum program and comparing the results with the analytical (pen-and-paper) calculations we have just derived.

This could be achieved by executing manually through the IDE, selecting the Classiq simulator as execution hardware, and setting Num shots to "100000":

gif execution of the Hadamard test using the Classiq simulator

Or through the SDK, by running the following code:

qmod = create_model(main)

tot_num_shots = 100000
quantum_model_with_execution_preferences = set_execution_preferences(
    qmod, num_shots=tot_num_shots
)
qprog = synthesize(quantum_model_with_execution_preferences)
job = execute(qprog)

results = job.result()[0].value.counts
P_0 = (results["0"]) / tot_num_shots
P_1 = (results["1"]) / tot_num_shots
print(r"P_0={}".format(P_0))
print(r"P_1={}".format(P_1))

P_0=0.62568
P_1=0.37432

Execution through the SDK enables post-processing of the data, allowing us to recover the real part of the expectation value and compare it to the analytically calculated value:

Expectation_value = 2 * P_0 - 1
print("Re(<U>)={}".format(Expectation_value))

Re(<U>)=0.25136000000000003

The value obtained is a statistical estimate derived from averaging measurement outcomes, where the number of measurements (tot_num_shots) determines the precision of this estimate.

Optional Exercise

Run the above example of the Hadamard Test for the QFT and the $|0000\rangle$ state from the SDK using 1,000, 2,000, 4,000, 8,000 and 16,000 shots. For each job, calculate the real part of the expectation value using the formula $\text{Re}\big(\langle{0000}|U_{QFT}|\rangle{0000}\big) = 2P_0-1$. Plot a graph of the expectation value as a function of the number of shots. Add to the graph the theoretical value. Explain the results. What is the mean and the variance for each execution? Why is that?

NOTE: Precision of the Results (read only after completing the exercise)

Increasing the tot_num_shots parameter in the execution preferences will enhance the precision of the expectation value estimation. This improvement arises from the statistical nature of the measurements; each measurement represents a sample from a distribution modeled by a classical random variable, with the expectation value corresponding to the mean of this distribution. As a result, the law of large numbers applies, and the standard error of the sample mean $ \langle U \rangle$ is inversely proportional to the square root of the sample size:

\[\sigma_{\langle U\rangle}=\frac{\sigma}{\sqrt{n}}\]

Where $\sigma $ is the standard deviation of the random variable modeling the measurements, and $ n $ represents the total number of measurements (tot_num_shots). This formula demonstrates that increasing the number of measurements reduces the statistical error of the estimated mean, resulting in a more reliable estimation of $ \langle U \rangle$

Mathematical Description

The following mathematical description is for an implementation of a Hadamard test on a system of one control qubit and a target qubit-array of $N$ qubits, initiated in $|{0}\rangle|{\psi}\rangle$, where $|{\psi}\rangle$ may essentially be in any prepared state.

The control qubit is first prepared in a uniform superposition by applying a Hadamard transform $H$:

\[|{\phi_1}\rangle=\big(H\otimes\mathbb{I}\big)|{0}\rangle|{\psi}\rangle= \frac{1}{\sqrt{2}}\Big(|{0}\rangle|{\psi}\rangle+|{1}\rangle|{\psi}\rangle\Big) \qquad\qquad;\qquad\qquad H=\frac{1}{\sqrt{2}}\left( {\begin{array}{cc} 1 & 1 \\ 1 & -1 \\ \end{array} } \right)\]

This step is sequentially followed by a selection step, in which a controlled unitary operation of the form $V=|{0}\rangle\langle{0}|\otimes \mathbb{I}+|{1}\rangle\langle{1}|\otimes U$ is successively applied to the target qubit(s), where $U$ is some general unitary matrix:

\[|{\phi_2}\rangle=V|{\phi_1}\rangle= |{0}\rangle U|{\psi}\rangle+|{1}\rangle|{\psi}\rangle\]

Another Hadamard transform is then applied to the control qubit:

\[|{\phi_3}\rangle=\big(H\otimes\mathbb{I}\big)|{\phi_2}\rangle= \frac{1}{2}\Big(|{0}\rangle|{\psi}\rangle+|{1}\rangle|{\psi}\rangle+|{0}\rangle U|{\psi}\rangle-|{1}\rangle U|{\psi}\rangle\Big)=\frac{1}{2}\Big(|{0}\rangle\big(\mathbb{I}+U\big)|{\psi}\rangle+|{1}\rangle\big(\mathbb{I}-U\big)|{\psi}\rangle\Big)\]

The final step, prior to the post-processing algebraic manipulation, is a projective measurement of the control (ancilla) qubit onto the $|{0}\rangle$ subspace $\mathcal{P}=|{0}\rangle\langle{0}|\otimes\mathbb{I}$:

\[|{\phi_4}\rangle=\mathcal{P}|{\phi_3}\rangle=\big(|{0}\rangle\langle{0}|\otimes\mathbb{I}\big)|{\phi_3}\rangle=\frac{1}{2}|{0}\rangle\big(\mathbb{I}+U\big)|{\psi}\rangle\]

This measurement is effectively translated into a measurement of the expectation value $\text{Re}\big(\langle{\psi}|U|{\psi}\rangle\big)$ by first obtaining the probability that the control qubit is in the $|{0}\rangle$ state:

\[P(0)=||\frac{1}{2}\big(\mathbb{I}+U\big)|{\psi}\rangle||^2=\frac{1}{4}\langle{\psi}|\big(\mathbb{I}+U^\dagger\big)\big(\mathbb{I}+U\big)|{\psi}\rangle=\frac{1}{4}\Big(\langle{\psi}|{\psi}\rangle+\langle{\psi}|U^\dagger|{\psi}\rangle+\langle{\psi}|U|{\psi}\rangle+\langle{\psi}|UU^\dagger|{\psi}\rangle\Big)=\frac{1}{4}\Big(2+\langle{\psi}|U^\dagger|{\psi}\rangle+\langle{\psi}|U|{\psi}\rangle\Big)\]

And algebraically manipulating it to receive the real part of the expectation value of $U$:

\[2P(0)-1=\frac{1}{2}\Big(2+\langle{\psi}|U^\dagger|{\psi}\rangle+\langle{\psi}|U|{\psi}\rangle\Big)-1=\frac{1}{2}\Big(\langle{\psi}|U^\dagger|{\psi}\rangle+\langle{\psi}|U|{\psi}\rangle\Big)=\frac{1}{2}\Big(\big(\langle{\psi}|U|{\psi}\rangle\big)^\dagger+\langle{\psi}|U|{\psi}\rangle\Big)=\text{Re}\big(\langle{\psi}|U|{\psi}\rangle\big)\]

All the Code Together

from classiq import *


@qfunc
def controlled_qft(expectation_value: QBit, psi: QArray):
    control(expectation_value, lambda: qft(psi))


@qfunc
def preparation_and_application(expectation_value: QBit, psi: QArray):
    within_apply(
        within=lambda: H(expectation_value),
        apply=lambda: controlled_qft(expectation_value, psi),
    )


@qfunc
def main(expectation_value: Output[QBit]):
    psi = QArray("psi")
    allocate(out=expectation_value, num_qubits=1)
    allocate(out=psi, num_qubits=4)
    preparation_and_application(expectation_value, psi)


qmod = create_model(main)
tot_num_shots = 100000
quantum_model_with_execution_preferences = set_execution_preferences(
    qmod, num_shots=tot_num_shots
)
qprog = synthesize(quantum_model_with_execution_preferences)
job = execute(qprog)

results = job.result()[0].value.counts
P_0 = (results["0"]) / tot_num_shots
P_1 = (results["1"]) / tot_num_shots
print(r"P_0={}".format(P_0))
print(r"P_1={}".format(P_1))

Expectation_value = 2 * P_0 - 1
print("Re(<U>)={}".format(Expectation_value))

write_qmod(qmod, "hadamard_test")

P_0=0.62556
P_1=0.37444
Re(<U>)=0.25112

References

[1]: Lecture Notes on Quantum Algorithms (Andrew M. Childs)

[2]: Quantum error mitigation for Fourier moment computation (Kiss et al.)

[3]: Quantum-classical algorithms for skewed linear systems with an optimized Hadamard test (Wu et al.)