Skip to content

Design - Classical Variables and Operations

View on GitHub Experiment in the IDE

Classical variables and operations lie at the heart of the Qmod language, but they are complemented by classical control flow and operations, making it easier to design quantum algorithms with hybrid quantum-classical logic. With the latest updates, Qmod now fully supports Python's classical operations, such as for loops, if-else statements, and more, smoothly integrating with quantum workflows.

In Qmod, equivalent types for common Python int, float, list, and bool types are denoted by int, real, array, and bool in the native syntax and by CInt, CReal, CArray, and CBool in the Python SDK. The Qmod types can be used in quantum workflows, though Python types can also be passed as classical parameters. For example, when writing quantum workflows, it is possible to use both the length of a quantum array, which is a Qmod quantity, or a Python int quantity to control the action of a loop. This ensures the type consistency required for quantum control flow operations like repeat (the Qmod equivalent of a Python for loop) and if-else statements, which enable sophisticated hybrid control logic, see a detailed description. Additionally, Qmod supports arrays of classical values and more configurable data structures called Structs (equivalent to Python dataclasses without methods). See the full list of classical variables and types supported in Qmod.

While Qmod enables the integration of Python types within its quantum workflows, the converse is not true with the capabilities covered so far. Python control flow constructs, such as range, for loops and if-else statements, cannot yet incorporate Qmod-specific quantities such as the len of a quantum array, within Python’s native control flow. Qmod quantities remain tightly integrated within the Qmod execution environment and cannot directly influence Python logic, ensuring a clear separation between classical Python constructs and Qmod quantum operations.

Generative Functions in Qmod

Generative functions in Qmod offer a powerful way to create and manipulate classical objects of Qmod with Python constructs. These functions allow the interaction between quantum and classical variables, enabling advanced logic and operations. Currently, it is possible to benefit from the following Python features within quantum programs using generative functions:

  • range: Generate sequences of classical values to iterate quantum operations dynamically over classical types within Qmod types.

  • if statements: Define conditional logic for generating and applying quantum operations using Qmod types as classical control parameters.

  • Treating quantum constants as classical: Converts parameters intricate to the quantum systems to Python types. This allows one to use, for example, integration of functions from external packages such as math.sqrt over classical quantities of a quantum object, such as the len of a quantum array.

Generative functions provide an elegant way to manage hybrid classical-quantum workflows, enhancing the expressiveness of your quantum algorithms. For more details and examples, refer to the Generative Functions documentation.

To enable generative functions in quantum function, it is necessary to modify the @qfunc decorator to @qfunc(generative=True).

First Example: State preparation

The task is to create a quantum array with \(10\) qubits in the state of \(|1010101010\rangle\); i.e., a quantum state with alternating qubit states of zeros and ones.

The way of doing this is based on knowing that a general qubit array can be easily initialized to the state of all zeros; i.e., \(|0000000000\rangle\), it should be sufficient to flip the state of every all the qubits in an even position (the qubits in the \(0th\) position, \(2nd\) position, \(4th\) position, etc.).

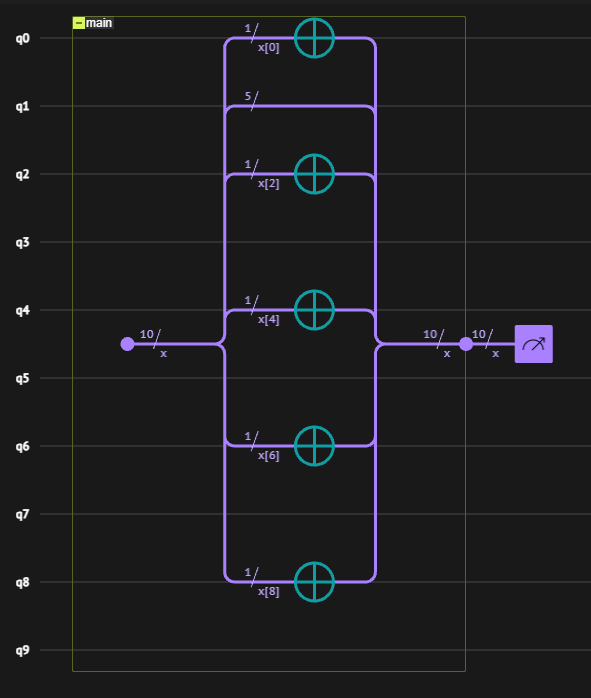
The argument of the main function is a qubit array named x. Initalize it to the state \(|0000000000\rangle\) with \(10\) qubits using the allocate function.

After that, by allowing generative functions by setting @qfunc(generative=True), it is possible to use the length of the qubit array x as a classical variable, and apply quantum operations over qubits dynamically, using Python's if and for statements over the qmod x.len quantity, according to the pre-defined rule of flipping the state of the even qubits.

The condition of whether i is even evaluated is using the % modulo operation, which calculates the reminder of the integer i divided by \(2\).

from classiq import *


@qfunc(generative=True)
def main(x: Output[QArray]):
    allocate(10, x)
    print(x.len)
    for i in range(x.len):
        if i%2==0:
            X(x[i])

That's it, the algorithm can be synthesized and viewed in the IDE:

quantum_program = synthesize(create_model(main))
show(quantum_program)

10
Opening: https://platform.classiq.io/circuit/c66bf31f-0016-4690-bca5-6a0959df4599?version=0.60.1

Evaluate the results by executing the quantum program on the default simulator:

results = execute(quantum_program).result()[0].value
print(results.counts)

{'0101010101': 2048}

The only measured bit string is \(0101010101\), which in Classiq notation is read from right to left when interpreted. Hence, it corresponds to the \(|1010101010\rangle\) state, which is exactly the target state.

State preparation: Slicing qubits

In this example, the task is to prepare the \(N\)-qubit state \(|00011111000\dots\rangle\), where the state \(|1\rangle\) is prepared in the qubits over the integer interval \((N/3, N/2)\). For this, it is possible to create a program that apply alternately the \(X\) operation to the correct qubits. In this example, consider a total of \(N=24\) qubits.

from classiq import *
@qfunc(generative=True)
def main(x: Output[QArray]):
    allocate(24, x)
    k=0
    for i in range(x.len//3,x.len//2):
        X(x[i])

quantum_program = synthesize(create_model(main))
show(quantum_program)

Opening: https://platform.classiq.io/circuit/8a864834-32a8-445e-a0e0-e38515edf8c1?version=0.60.1

Summary - Classical Variables and Operations

Key features of this tutorial:

  • Classical data types: Data types int, real, and bool are denoted as CInt, CReal, and CBool in the Python SDK. Complex structures like arrays and Structs (similar to Python dataclasses) are also supported.

  • Quantum control flow: Qmod fully supports Python types such as float, int and bool variables within Qmod control flow, such as repeat and if-for statements.

Generative Functions in Qmod

Generative functions are employed to enhance hybrid quantum-classical workflows by treating quantum objects into classical variables:

  • Dynamic iteration: Using range and for loops integration with Qmod types, such as len.

  • Conditional operations: Using if statements controlled by Qmod types.