Skip to content

Execute

View on GitHub Experiment in the IDE

The last step of the quantum algorithm development process using Classiq is to execute the quantum program on a quantum computer or a simulator. You can do it in the IDE or through the Python SDK. Classiq offers access to a wide variety of quantum computers with different hardware modalities from companies including IonQ, Quantinuum, IBM, OQC, and Rigetti, as well as several simulators.

The execution phase comprises configuration and access to the results. This page covers these steps using a concrete example, starting with the default Classiq execution options for the execution you encountered in the previous example of this 101 guide.

Default Execution

Continuing with the algorithm you already encountered, create a quantum algorithm that calculates the arithmetic expression \(y=x^2+1\) in a superposition. The algorithm, written in Qmod, implements this task:

from classiq import *


@qfunc
def main(x: Output[QNum], y: Output[QNum]):

    allocate(4, x)
    hadamard_transform(x)  # creates a uniform superposition
    y |= x**2 + 1

Synthesize the algorithm:

quantum_program = synthesize(create_model(main))

Execute the quantum program directly and analyze the results:

job = execute(quantum_program)
results = job.result()[0].value.parsed_counts
print(results)

[{'x': 0.0, 'y': 1.0}: 91, {'x': 5.0, 'y': 26.0}: 72, {'x': 10.0, 'y': 101.0}: 71, {'x': 2.0, 'y': 5.0}: 71, {'x': 15.0, 'y': 226.0}: 68, {'x': 14.0, 'y': 197.0}: 67, {'x': 12.0, 'y': 145.0}: 66, {'x': 11.0, 'y': 122.0}: 64, {'x': 9.0, 'y': 82.0}: 61, {'x': 1.0, 'y': 2.0}: 60, {'x': 13.0, 'y': 170.0}: 60, {'x': 4.0, 'y': 17.0}: 59, {'x': 6.0, 'y': 37.0}: 49, {'x': 8.0, 'y': 65.0}: 47, {'x': 3.0, 'y': 10.0}: 47, {'x': 7.0, 'y': 50.0}: 47]

The code above demonstrates how to execute using the default Classiq configuration, which executes on a simulator (of up to 25 qubits) with 1,000 shots. Now see how to execute with other configurations.

Configuring the Execution

Configuration in the IDE

In the IDE, during the visualization of the quantum program, configure the execution by clicking Execute. The Execution tab opens:

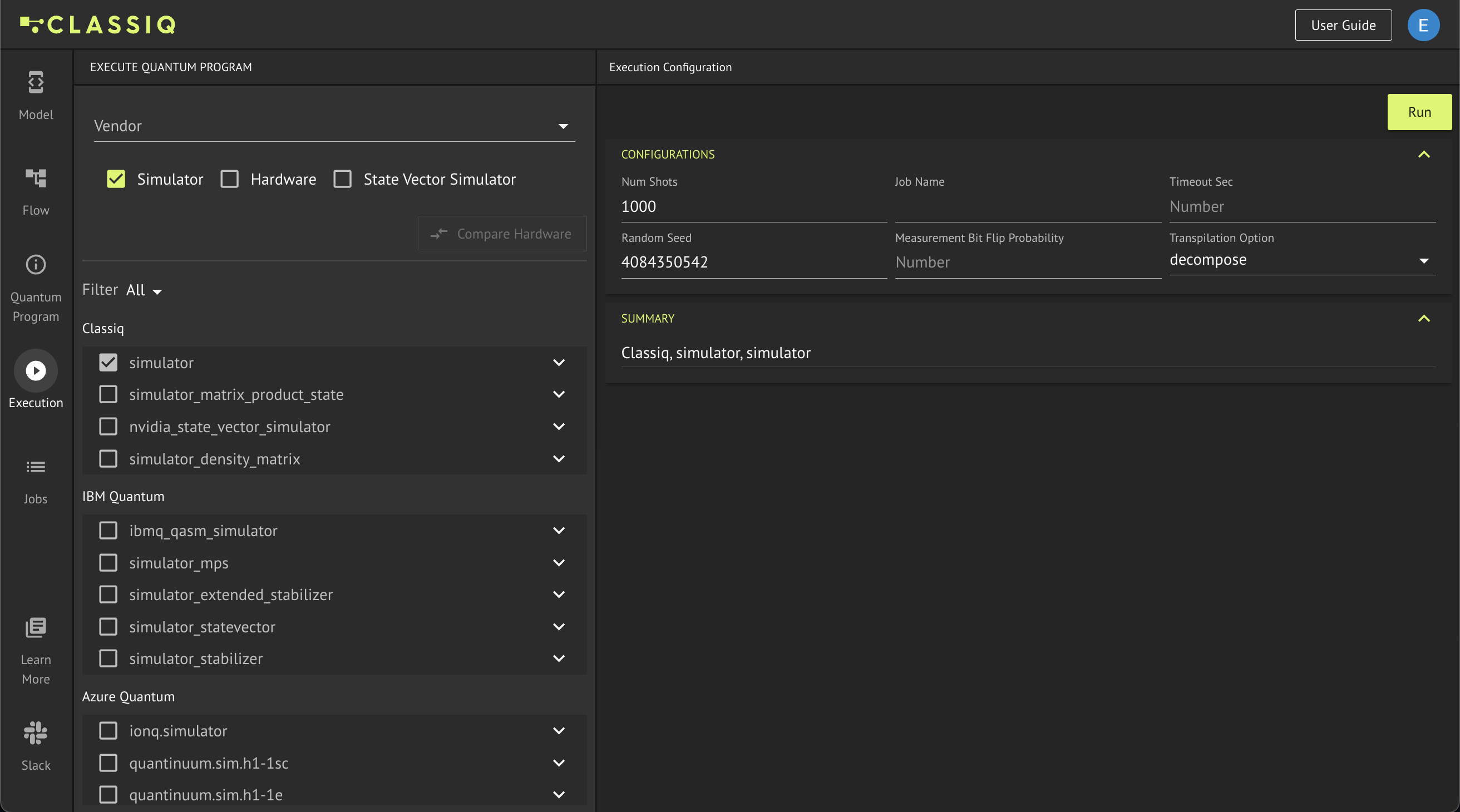
On the left is a list of the available simulators. To see a list of the hardware available via the platform, select the Hardware box at the top of the window. When you click Run, you may need to specify vendor credentials for the hardware and some of the simulators to enable access to the relevant computing resources. (See details in the reference manual.)

On the right, you can configure the specific execution:

  • Num Shots is the number of shots the quantum program samples.

  • Job Name specifies the name of the job.

  • Random Seed requests receiving exactly the same results when using a simulator (as well as more advanced execution options on real hardware such as variational quantum algorithms and advanced transpilation methods).

When you finish the configuration, click Run.

Configuration in the SDK

You can also configure the execution from the SDK, by adapting the quantum model to your execution preferences, similarly to the constraints and preferences from the optimization phase.

This code demonstrates how to change the number of shots, specify a name for the job, and set a random seed for the simulator:

from classiq.execution import ExecutionPreferences

quantum_model = create_model(main)
quantum_model_with_execution_preferences = set_execution_preferences(
    quantum_model,
    ExecutionPreferences(
        num_shots=2048, job_name="classiq 101 - execute", random_seed=767
    ),
)

Synthesize and execute the adapted quantum model:

quantum_program_with_execution_preferences = synthesize(
    quantum_model_with_execution_preferences
)
job = execute(quantum_program_with_execution_preferences)

See the full list of configuration options for the execution preferences in the reference manual.

Accessing the Results

Results in the IDE

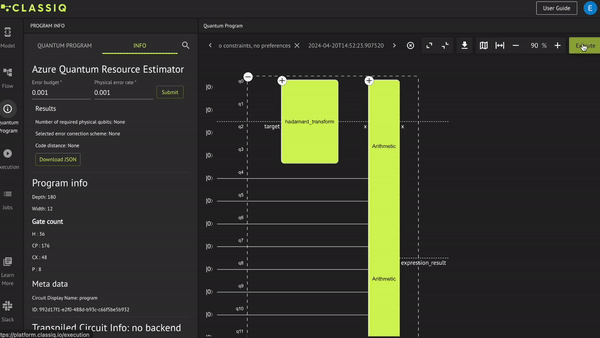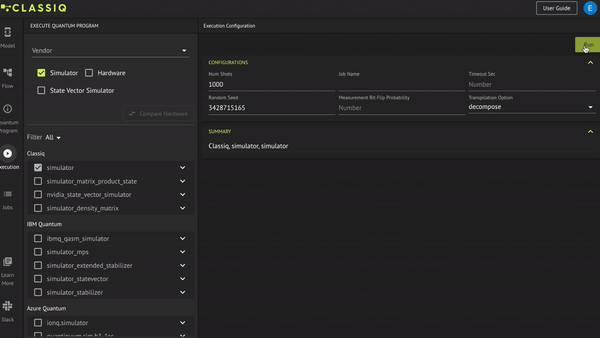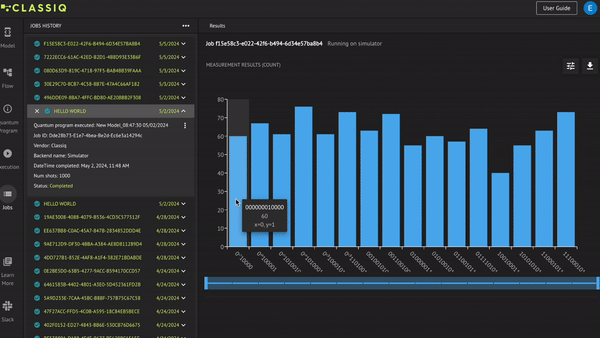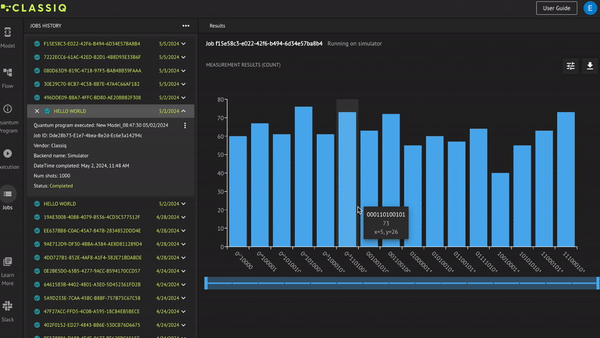
When you click Run in the Execution tab, the Jobs tab opens. All your jobs are listed on the left of the window. To view the information for a specific job, click it.

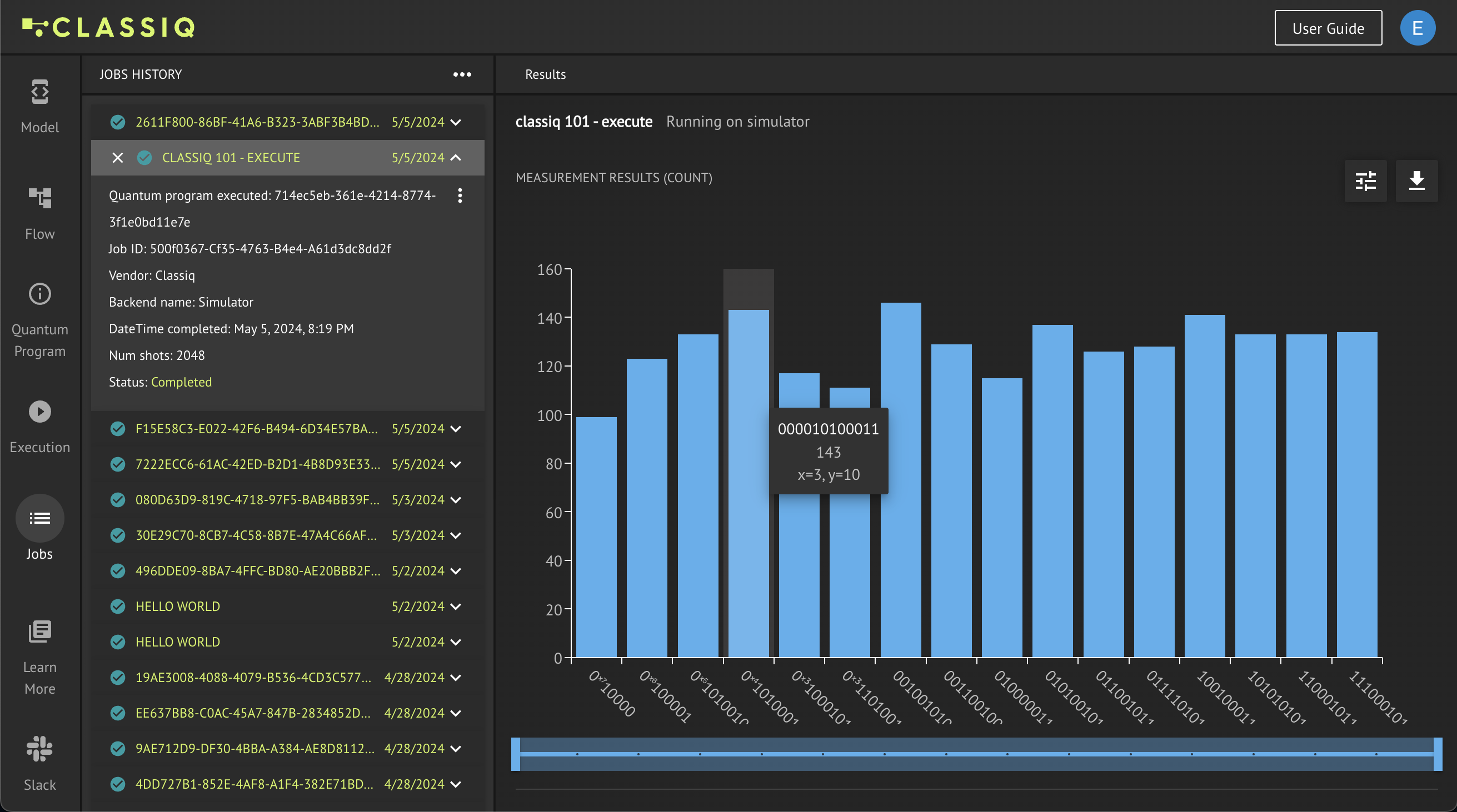
The histogram of the results is on the right. Each bin represent a specific measurement result and its height represents the counts of that measurement. Hover over a specific bin to see the variables of the measurement results and the counts of that bin.

In the top right corner are two buttons. The left button suggests further options for analyzing the histogram results and the right one downloads the results of the job in a specific format such as .csv.

Results in the SDK

The job variable is the output of the Execute command. It contains all the data about the execution job. You can access some of the metadata directly from this object:

print(
    f"The job on the provider {job.provider} on the backend {job.backend_name} with {job.num_shots} shots is {job.status}. Access it in the IDE via this URL: {job.ide_url}"
)

The job on the provider Classiq on the backend simulator with 2,048 shots is QUEUED. Access it in the IDE via this URL: https://platform.classiq.io/jobs/ea0fa2c8-515a-48cf-b8ce-c5e6f6c74803

In addition to the metadata, you can open the job directly in the IDE:

job.open_in_ide()

Access the actual results of the job:

results = job.result()[0].value

The results variable contains a dictionary of the measured variables and counts of the algorithm:

print(results.parsed_counts)

[{'x': 6.0, 'y': 37.0}: 146, {'x': 3.0, 'y': 10.0}: 143, {'x': 12.0, 'y': 145.0}: 141, {'x': 9.0, 'y': 82.0}: 137, {'x': 15.0, 'y': 226.0}: 134, {'x': 13.0, 'y': 170.0}: 133, {'x': 14.0, 'y': 197.0}: 133, {'x': 2.0, 'y': 5.0}: 133, {'x': 7.0, 'y': 50.0}: 129, {'x': 11.0, 'y': 122.0}: 128, {'x': 10.0, 'y': 101.0}: 126, {'x': 1.0, 'y': 2.0}: 123, {'x': 4.0, 'y': 17.0}: 117, {'x': 8.0, 'y': 65.0}: 115, {'x': 5.0, 'y': 26.0}: 111, {'x': 0.0, 'y': 1.0}: 99]

Access the raw bit strings directly:

print(results.counts)

{'000000100001': 123, '010100101001': 137, '000100010100': 117, '111000101111': 134, '000000010000': 99, '001100100111': 129, '000010100011': 143, '101010101101': 133, '000110100101': 111, '010000011000': 115, '001001010110': 146, '011110101011': 128, '100100011100': 141, '110001011110': 133, '000001010010': 133, '011001011010': 126}

Extract the direct mapping between the bit strings and the measured variables: 

print(results.parsed_states)

{'000000100001': {'x': 1.0, 'y': 2.0}, '010100101001': {'x': 9.0, 'y': 82.0}, '000100010100': {'x': 4.0, 'y': 17.0}, '111000101111': {'x': 15.0, 'y': 226.0}, '000000010000': {'x': 0.0, 'y': 1.0}, '001100100111': {'x': 7.0, 'y': 50.0}, '000010100011': {'x': 3.0, 'y': 10.0}, '101010101101': {'x': 13.0, 'y': 170.0}, '000110100101': {'x': 5.0, 'y': 26.0}, '010000011000': {'x': 8.0, 'y': 65.0}, '001001010110': {'x': 6.0, 'y': 37.0}, '011110101011': {'x': 11.0, 'y': 122.0}, '100100011100': {'x': 12.0, 'y': 145.0}, '110001011110': {'x': 14.0, 'y': 197.0}, '000001010010': {'x': 2.0, 'y': 5.0}, '011001011010': {'x': 10.0, 'y': 101.0}}

Extract the notation indicating whether the bit strings are interpreted with the least significant bit (LSB) on the right or left:

print(results.counts_lsb_right)

True

All the above options allow you to analyze the results and post-process them in Python as needed.

Adapt the code such that the quantum number \(x\) is allocated with 8 qubits. Then, execute the algorithm with 5096 shots and post process the results from your Python SDK. Plot a graph of all the measured values of \(x\) and \(y\) with the corresponding axes (make sure you receive the graph of \(y=x^2+1\)).

write_qmod(quantum_model_with_execution_preferences, "execute")